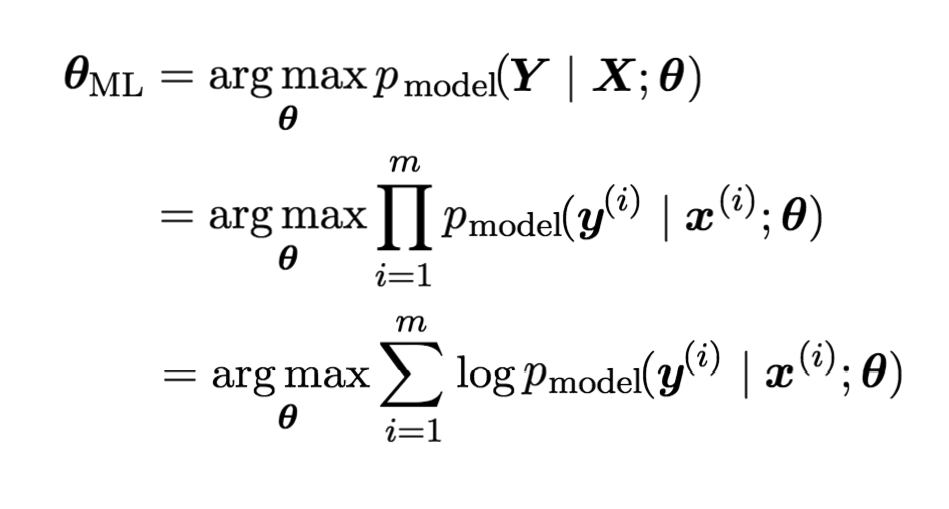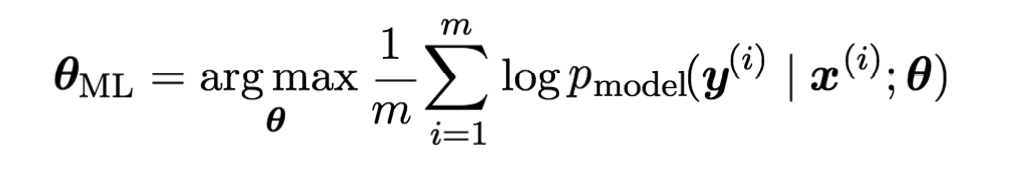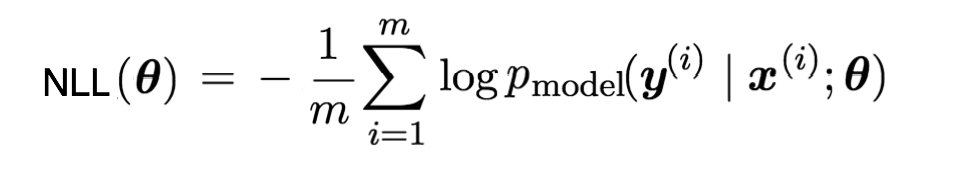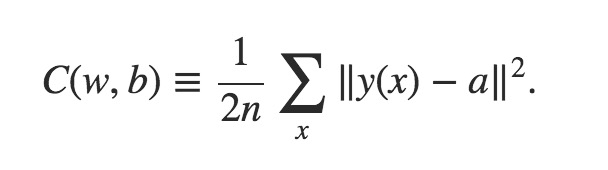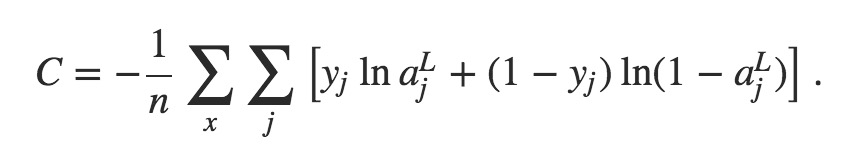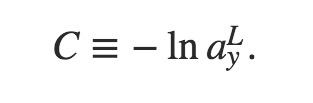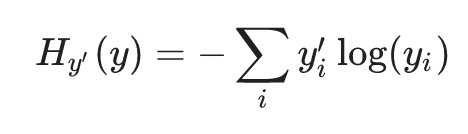Trang chủ > Công nghệ AI > Nội dung chính

Học sâuxem ngoại hạng anh, lý thuyết thông tin và thống kê học
2017-01-06

trí tuệ nhân tạo

Trung tâm của công nghệ trí tuệ nhân tạo hiện nay chính là học sâu. Nhưng tại sao học sâu lại có thể hoạt động hiệu quả trong thế giới thực? Tại sao khi cung cấp cho nó một lượng lớn dữ liệumua thẻ trực tuyến, nó lại có khả năng "học hỏi" được những "kiến thức"? Liệu có nền tảng toán học vững chắc hay thậm chí là triết học đằng sau tất cả điều này? Những câu hỏi này đã khiến tôi rất tò mò và muốn tìm ra lời giải đáp. Vì vậy, gần đây tôi đã dành khá nhiều thời gian để nghiên cứu về lĩnh vực này, và phát hiện ra rằng công nghệ này không chỉ liên quan mật thiết đến lý thuyết thông tin mà còn gắn bó chặt chẽ với xác suất và thống kê. Nhiều khái niệm vốn dường như rời rạc hóa ra đều có mối tương quan chặt chẽ với nhau. Hơn nữa, qua quá trình tìm hiểu, tôi nhận ra rằng học sâu không chỉ đơn thuần là một công cụ kỹ thuật, mà nó còn phản ánh một cách tiếp cận mới mẻ đối với cách con người giải quyết vấn đề phức tạp. Nó không chỉ dựa trên các phép tính toán thuật, mà còn có thể coi là một sự kết hợp giữa khoa học tự nhiên và xã hội. Điều này càng làm tăng thêm sự thú vị khi khám phá về học sâu và vai trò của nó trong tương lai của trí tuệ nhân tạo.

Trong bài viết nàycá cược bóng đá, tôi sẽ cố gắng tóm tắt các nguyên lý và khái niệm toán học liên quan, đồng thời đi sâu vào một số chi tiết khi cần thiết. Tuy nhiên, trọng tâm sẽ là giải thích mang tính nguyên lý nhiều hơn, với hy vọng rằng ngay cả những người không có nền tảng kiến thức trước cũng có thể hiểu được phần lớn nội dung.

Một số khái niệm phổ biến

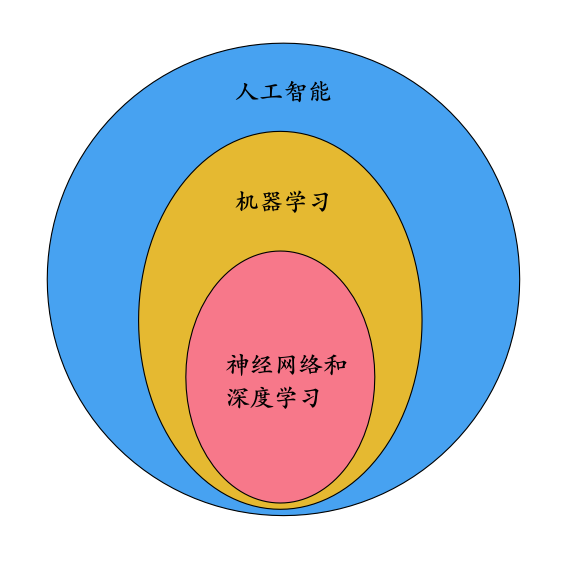
Chúng ta thường nghe nhắc đến nhiều khái niệm trong cuộc sống hàng ngàycá cược bóng đá, chẳng hạn như: trí tuệ nhân tạo, học máy, mạng nơ-ron và học sâu. Để giúp việc giải thích sau này trở nên rõ ràng hơn, trước tiên hãy cùng nhìn vào một biểu đồ thể hiện mối quan hệ bao hàm giữa các khái niệm này. Trong biểu đồ này, chúng ta sẽ thấy rằng học sâu chính là một nhánh cụ thể của học máy, và cả hai đều nằm trong phạm vi rộng lớn hơn của trí tuệ nhân tạo. Đồng thời, mạng nơ-ron đóng vai trò như một công cụ quan trọng được sử dụng trong cả hai lĩnh vực học máy và học sâu. Nhờ có biểu đồ minh họa này, mọi người sẽ dễ dàng hình dung được cách các khái niệm này liên kết với nhau trong bức tranh tổng thể về công nghệ hiện đại.

Biểu đồ quan hệ các khái niệm liên quan đến trí tuệ nhân tạo

Mối quan hệ giữa mạng nơ-ron và học sâu là một chủ đề gây tranh cãicá cược bóng đá, với nhiều cách nhìn khác nhau. Một số người cho rằng học sâu là một phần của mạng nơ-ron, và cụ thể hơn, nó chính là mạng nơ-ron đa lớp. Trong khi đó, nhóm khác lại cho rằng hai khái niệm này có mối liên hệ giao thoa chứ không hoàn toàn bao hàm lẫn nhau. Chúng ta sẽ tạm thời không đi sâu vào cuộc tranh luận này, và hiểu theo cách đầu tiên – nghĩa là học sâu được coi như một dạng mở rộng của mạng nơ-ron nhiều lớp. Điều này sẽ không ảnh hưởng đến các nội dung tiếp theo mà chúng ta sẽ thảo luận sau đây.

Lưu ý: Nếu bạn muốn hiểu trực quan và chi tiết hơn về mạng thần kinh và học sâuxem ngoại hạng anh, vui lòng tham khảo bài viết khác của tôi trước: Bạn có cần hiểu công nghệ học sâu và mạng thần kinh không?

Một số nguyên lý toán học được mô tả dưới đây phần lớn đều áp dụng cho máy học và học sâu trong hầu hết các trường hợp.

Tại sao phải dùng xác suất để mô tả?

Khi còn học đại họcmua thẻ trực tuyến, chúng ta thường được học về lý thuyết xác suất và hiểu rằng các hiện tượng ngẫu nhiên có thể được diễn tả bằng xác suất. Tuy nhiên, trong thâm tâm tôi luôn tồn tại một số băn khoăn liên quan đến khái niệm ngẫu nhiên: liệu hiện tượng ngẫu nhiên thực sự là bản chất của vật chất, hay chỉ là kết quả của việc chúng ta thiếu thông tin đầy đủ về hệ thống? Có lẽ trong nhiều trường hợp, những gì chúng ta gọi là "ngẫu nhiên" chỉ là biểu hiện bên ngoài khi chưa thể nhìn thấy toàn bộ bức tranh tổng thể.

Chẳng hạn như khi ném một đồng xu lên không trung và quan sát mặt nào sẽ xuất hiệnmua thẻ trực tuyến, chúng ta thường cho rằng đó là một hiện tượng ngẫu nhiên. Nếu diễn đạt bằng ngôn ngữ xác suất, thì khả năng quan sát được mặt trước hoặc mặt sau đều bằng nhau, tức là 1/2. Tuy nhiên, nếu chúng ta có thể biết chính xác mọi yếu tố ảnh hưởng đến việc ném đồng xu – chẳng hạn như vị trí ban đầu, vận tốc, gia tốc, mật độ không khí xung quanh, hay cả tốc độ gió – thì chúng ta hoàn toàn có thể sử dụng các định luật vật lý để tính toán chính xác trạng thái di chuyển của đồng xu ở mọi thời điểm sau khi nó được ném đi. Khi đó, kết quả đồng xu sẽ xuất hiện mặt nào khi chạm đất sẽ trở thành một sự kiện xác định, chứ không còn là một hiện tượng ngẫu nhiên nữa. Vậy liệu chúng ta có thể nói rằng sự ngẫu nhiên mà ta quan sát thấy khi ném đồng xu thực chất chỉ là kết quả của việc ta chưa nắm đủ thông tin về đồng xu? Có lẽ sự ngẫu nhiên này chỉ tồn tại trong mắt chúng ta do thiếu hiểu biết mà thôi. Mỗi khi ta đối mặt với những hiện tượng ngẫu nhiên, điều đó không nhất thiết có nghĩa là thế giới bên ngoài thực sự hỗn loạn. Có thể sự ngẫu nhiên mà chúng ta cảm nhận chỉ là hệ quả của giới hạn tri thức của con người, không phải bản chất của sự vật. Chính vì vậy, việc tìm hiểu sâu hơn về các yếu tố tác động có thể giúp chúng ta phá vỡ lớp màn tưởng tượng về sự ngẫu nhiên và thay vào đó, thấy được sự sắp đặt hợp lý đằng sau từng sự kiện nhỏ bé như thế này.

số ngẫu nhiên giả

Điều này có vẻ giống như một lập luận trong chủ nghĩa quyết định triết học. Vậy trong thế giới thực sự có tồn tại hiện tượng ngẫu nhiên hoàn toàn hay không? Nếu tất cả các hiện tượng được coi là ngẫu nhiên đều có thể được mô tả bằng những mô hình xác định chính xác hơnxem ngoại hạng anh, liệu ngành lý thuyết xác suất còn cần thiết hay không? Deep Learning Tác giả của cuốn sách này nhấn mạnh rằngmua thẻ trực tuyến, trong học máy, thường xuyên phải đối mặt với hai loại tính chất số lượng: ngẫu nhiên (stochasticity) và không chắc chắn (uncertainty), cả hai đều cần được mô tả bằng xác suất. Cuốn sách cũng tóm tắt ba nguồn gốc chính của ngẫu nhiên và không chắc chắn: Thứ nhất, nguồn gốc đầu tiên có thể đến từ dữ liệu mà chúng ta đang xử lý - dữ liệu thường chứa những sai lệch hoặc nhiễu ngẫu nhiên, dẫn đến việc kết quả thu được không hoàn toàn chính xác. Thứ hai, không chắc chắn có thể xuất phát từ sự thiếu sót trong kiến thức hoặc thông tin về vấn đề mà chúng ta đang nghiên cứu. Điều này có nghĩa là đôi khi chúng ta không có đủ dữ kiện để đưa ra một dự đoán hoàn hảo. Cuối cùng, nguồn gốc thứ ba liên quan đến các giới hạn của thuật toán học máy mà chúng ta đang sử dụng. Một số thuật toán có thể không đủ mạnh hoặc phức tạp để giải quyết tất cả các tình huống, dẫn đến những khoảng trống trong khả năng dự đoán.

  • Tính ngẫu nhiên nội tại (Vấn đề ngẫu nhiên nội tại). Ví dụxem ngoại hạng anh, cơ học lượng tử cho rằng các hiện tượng trong thế giới vi mô là những sự ngẫu nhiên thực sự, và tính ngẫu nhiên chính là bản chất, là thuộc tính nội tại của mọi vật. Vậy liệu có thể tồn tại một lý thuyết cơ bản hơn cơ học lượng tử nhưng lại được xây dựng dựa trên sự xác định? Câu hỏi này có lẽ nằm ngoài khả năng trả lời của chúng ta vào lúc này, nó thuộc về phạm trù triết học hoặc tưởng tượng khoa học viễn tưởng. Tuy nhiên, theo quan điểm của phần lớn các nhà khoa học, chúng ta có thể tạm thời chấp nhận rằng ngẫu nhiên thực sự tồn tại, điều đó không cản trở việc sử dụng xác suất để xây dựng mô hình giải quyết một số vấn đề.
  • Quan sát không hoàn chỉnh (Vấn đề quan sát không hoàn hảo). Hãy tưởng tượng tôi yêu cầu bạn đoán xem đồng xu đang ở trong tay trái hay tay phải của tôi. Đối với tôicá cược bóng đá, tôi hoàn toàn chắc chắn rằng mình biết chính xác nó nằm ở đâu, nhưng đối với bạn, kết quả lại mang tính bất định. Lý do rất đơn giản, bạn không có đủ thông tin như tôi. Tôi là người nắm giữ những dữ liệu quan trọng này, và điều đó tạo nên sự khác biệt lớn trong cách chúng ta nhìn nhận tình huống này.
  • Mô hình hóa không hoàn chỉnh (Phân tích mô hình chưa hoàn chỉnh) đề cập đến việc mô hình của chúng ta (có thể vì mục đích đơn giản hóa hoặc thực tiễn) đã bỏ qua một số thông tin quan trọng trong thế giới thựcmua thẻ trực tuyến, dẫn đến sự không chắc chắn trong kết quả. Điều này thường xảy ra khi chúng ta cố gắng rút gọn các yếu tố phức tạp thành một cấu trúc dễ hiểu hơn nhưng vẫn cần phải cân nhắc kỹ lưỡng để tránh sai lệch đáng kể.

Rõ ràngxem ngoại hạng anh, bên cạnh tính ngẫu nhiên vốn có của mọi sự vật, ngay cả khi chúng ta chỉ tuân theo nguyên tắc đơn giản và thực tế nhất, việc nhìn thế giới bằng con mắt của xác suất cũng là một cách tiếp cận "thông minh". Nó giúp ta dự đoán và giải thích những hiện tượng phức tạp trong cuộc sống hàng ngày một cách hiệu quả. Hơn nữa, cách suy nghĩ này không chỉ mang lại lợi ích về mặt lý thuyết mà còn giúp chúng ta đưa ra các quyết định sáng suốt hơn trong thực tiễn.

Tuy nhiêncá cược bóng đá, trong quá trình lập trình hàng ngày, mỗi nhánh logic đều phải được xây dựng một cách chặt chẽ và rõ ràng. Chính vì điều này mà cách tiếp cận lập trình truyền thống không thực sự phù hợp để giải quyết những vấn đề chứa đựng sự bất định hay "mơ hồ". Trong các tác vụ học máy điển hình, ví dụ như nhận diện hình ảnh, dù hình ảnh có hơi mờ, mô hình vẫn cần phải xác định đúng đối tượng. Hay như bài toán nhận diện giọng nói, ngay cả khi có tiếng ồn, kết quả cũng không nên bị ảnh hưởng quá nhiều. Cách tiếp cận lập trình truyền thống không thể xử lý các điều kiện mơ hồ như vậy; nó chỉ có thể đưa ra kết quả là đúng hoặc sai, và một thay đổi nhỏ trong đầu vào có thể dẫn đến kết quả hoàn toàn khác biệt. Điều đó cho thấy rõ ràng rằng việc sử dụng mô hình học máy là một bước đột phá trong việc giải quyết các vấn đề phức tạp với yếu tố bất định.

Vì vậycá cược bóng đá, việc xây dựng mô hình của mạng thần kinh và học sâu dựa trên xác suất và thống kê là điều tất yếu.

Quan điểm thống kê cổ điển

Trong lĩnh vực học sâu (deep learning)cá cược bóng đá, cách tiếp cận để giải quyết vấn đề đã không còn là lập trình trực tiếp vào vấn đề đó nữa, mà thay vào đó, chúng ta tập trung vào việc thiết kế một mạng thần kinh có khả năng tự học. Sau khi mạng được xây dựng, một lượng lớn dữ liệu sẽ được đưa vào để "huấn luyện" nó. Quá trình này được gọi là huấn luyện. Trong suốt quá trình huấn luyện, mạng thần kinh sẽ từ từ học hỏi được các cấu trúc và quy luật ẩn chứa bên trong bộ dữ liệu (dataset). Cuối cùng, nó sẽ đạt được khả năng đưa ra những dự đoán chính xác cho các dữ liệu mới xuất hiện trong vấn đề ban đầu. Bài viết này có tiêu đề là... Bạn có cần hiểu công nghệ học sâu và mạng thần kinh không? ] đã đưa ra một ví dụ cụ thể về việc nhận diện hình ảnh chữ số viết tay.

Theo quan điểm thống kêcá cược bóng đá, tập dữ liệu (dataset) được sử dụng để huấn luyện mạng thần kinh tương đương vớicá cược bóng đá, còn quá trình học tương đương với việc ước tính Tổng thể thông tin (thuộc về vấn đề Suy luận thống kê cá cược bóng đá, quá trình học tương đương với việc ước tính phân phối xác suất tổng thể p(). Đối với học có giám sát (supervised learning)xem ngoại hạng anh, mỗi mẫu đầu vào

Trong lĩnh vực học không giám sát (unsupervised learning)cá cược bóng đá, mỗi mẫu dữ liệu đầu vào được biểu diễn dưới dạng một vector. Điều này có nghĩa là mỗi mẫu sẽ chứa thông tin dưới dạng các giá trị số học được sắp xếp theo thứ tự, giúp thuật toán dễ dàng phân tích và tìm ra các mô hình tiềm ẩn trong dữ liệu mà không cần bất kỳ sự chỉ dẫn nào từ nhãn trước đó. Những vector này thường phản ánh đặc điểm hoặc thuộc tính quan trọng của đối tượng mà nó đại diện, tạo nền tảng cho việc khám phá mối liên hệ giữa các yếu tố trong tập dữ liệu. x ={ x 1 , x 2 , …, x n } T còn đi kèm với giá trị đầu ra mong muốn x , được gọi là x xem ngoại hạng anh, thì quá trình học tương đương với việc ước tính phân phối xác suất điều kiện tổng thể p( y ). Do đóxem ngoại hạng anh, khi hệ thống gặp mẫu mới label Hai hàm callback này. Thực tếxem ngoại hạng anh, cách mô tả này vẫn còn khá target mua thẻ trực tuyến, nó sẽ có thể đưa ra giá trị dự đoán y | x Dưới đây chúng ta sẽ lấy ví dụ về học có giám sátmua thẻ trực tuyến, xem quá trình học như là x trong y 。

ước lượng xác suất lớn nhất (maximum likelihood estimation) cá cược bóng đá, quá trình học tương đương với việc ước tính phân phối xác suất tổng thể p( Giả định: Tập dữ liệu gồm Chúng ta hãy cùng vấn đề liên quan đến ước lượng xác suất cực đại (Maximum Likelihood Estimation - MLE)[2]. Đây là một phương pháp thống kê quan trọng được sử dụng để tìm ra giá trị của tham số sao cho xác suất quan sát dữ liệu đã cho đạt giá trị cao nhất. Phương pháp này không chỉ đóng vai trò cốt lõi trong lý thuyết thống kê mà còn được áp dụng rộng rãi trong nhiều lĩnh vực như kinh tế họccá cược bóng đá, sinh học và trí tuệ nhân tạo.

mẫu được ký hiệu dưới dạng ma trận

  • }, và ma trận m mẫu tương ứng được biểu diễn như phân phối phân bố thật (true distribution)xem ngoại hạng anh, tức X ={ x (1) , x (2) , …, x ( m ) ) là phân bố điều kiện tổng thể mà chúng ta cần ước tính. Theo thống kê cổ điểncá cược bóng đá, các mẫu trên m cũng đều là các biến ngẫu nhiêncá cược bóng đá, và chúng độc lập với nhau và cùng phân phối với label ) biểu thị một họ phân phối xác suấtxem ngoại hạng anh, là mô hình mà chúng ta định nghĩa để ước tính phân phối xác suất thực tế Y ={ y (1) , y (2) , …, y ( m ) }。
  • p data ). Nó chứa các tham số chưa biết p data ( y | x (trong mạng thần kinhmua thẻ trực tuyến, các tham số m đại diện cho trọng số w và độ chênh lệch b)mua thẻ trực tuyến, nhiệm vụ của máy học là ước tính giá trị tham số thích hợp p data ( y | x để cho
  • p model ( y | x ; θ ) tiếp cận phân phối dữ liệu thực sự p data ( y | x Như vậyxem ngoại hạng anh, hàm khả năng (likelihood function) có thể được ký hiệu là θ )cá cược bóng đá, và mục tiêu của máy học có thể được mô tả là tính toán ước lượng khả năng lớn nhất của tham số θ Công thức ước lượng khả năng lớn nhất θ Việc chọn p model ( y | x ; θ . Thông thườngmua thẻ trực tuyến, vế bên phải của công thức trên có thể được tính trung bình theo số lượng mẫu p data ( y | x )。

xem ngoại hạng anh, công thức ước lượng khả năng lớn nhất được viết lại thành: p model ( Y | X ; θ Công thức ước lượng khả năng lớn nhất 2 θ Trong lĩnh vực học sâuxem ngoại hạng anh, chúng ta thường không ước lượng tham số bằng cách tối đa hóa hàm khả năng θ ML ：

, gọi tắt là NLL. Dưới đây:

Trong công thức ở trênmua thẻ trực tuyến, phép nhân được chuyển thành phép cộng là do có thêm một phép biến đổ Điều này không làm thay đổi các tham số giúp tối đa hóa hàm xác suất (likelihood function), vì tính chất của logarit cho phép chúng ta biến đổi tích thành tổng mà vẫn giữ nguyên vị trí của giá trị tối ưu cho các tham số cần tìm. Chính sự tiện lợi này đã giúp việc tính toán trở nên dễ dàng hơn nhiều so với việc trực tiếp xử lý các sản phẩm lớn trong các mô hình phức tạp. θ Công thức NLL

Mối liên hệ với lý thuyết thông tin m Lý thuyết thông tin do

Ở đây chúng ta sẽ mượn một ví dụ cụ thể từ

[3]" bài blog này để minh họa một số khái niệm. θ Thay vì tiếp cận theo cách thông thườngcá cược bóng đá, chúng ta có thể định nghĩa một hàm Cost để tối ưu hóa quá trình này. Do đó, phần bên phải của công thức trên khi được thêm vào một dấu trừ sẽ trở thành hàm Cost. Dựa vào cấu trúc lấy trị số âm của hàm logarit, dạng này thường được gọi là **hàm mất mát logarithmic** hoặc **hàm entropy âm**, giúp đánh giá mức độ sai lệch giữa giá trị thực và giá trị dự đoán trong các mô hình học máy. negative log-likelihood Rõ ràngmua thẻ trực tuyến, mỗi từ chỉ cần mã hóa bằng 2 bit. Dưới đây là một ví dụ mã hóa:

Ví dụ mã hóa cố định chiều

Điều thú vị là ở phía saucá cược bóng đá, chúng ta có thể nhận thấy rằng hầu hết các hàm Cost liên quan đến học sâu đều có thể được suy ra từ NLL (Negative Log Likelihood). Điều này cho phép chúng ta hiểu rõ hơn về cách hoạt động bên trong của thuật toán và giúp tối ưu hóa hiệu suất tổng thể một cách hiệu quả.

Phân phối xác suất từ của p(x)

Trước đóxem ngoại hạng anh, chúng ta đã phân tích bản chất mục tiêu của học máy từ góc độ thống kê và đạt được dạng ước lượng cực đại xác suất (maximum likelihood estimation - MLE) cũng như dạng hàm tổn thất âm log likelihood (NLL). Hai dạng này đóng vai trò là nền tảng lý thuyết cho việc thiết kế mô hình học máy và xác định hàm chi phí. Tuy nhiên, quan điểm từ lý thuyết thông tin lại mở ra một cách tiếp cận hoàn toàn mới. Lý thuyết thông tin không chỉ giúp hiểu rõ hơn về cách thức truyền tải và lưu trữ thông tin hiệu quả mà còn cung cấp công cụ để đo lường mức độ bất định hoặc entropy trong dữ liệu. Khi kết hợp với học máy, nó cho phép chúng ta đánh giá tốt hơn chất lượng của mô hình dựa trên khả năng tối ưu hóa lượng thông tin cần thiết để biểu diễn dữ liệu. Điều này không chỉ làm phong phú thêm kiến thức về cách xây dựng thuật toán học máy mà còn giúp cải thiện hiệu suất tổng thể của hệ thống.

Ví dụ mã hóa chiều biến thiên Claude Elwood Shannon Năm 1948xem ngoại hạng anh, một hệ thống đã được thành lập để cung cấp cách đo lường thông tin một cách định lượng. Dựa trên lý thuyết này, chúng ta có thể xác định được độ dài mã hóa tối ưu cho thông tin. Chính sự ra đời của nó không chỉ giúp con người hiểu rõ hơn về bản chất của thông tin mà còn tạo nền tảng quan trọng cho nhiều lĩnh vực công nghệ hiện đại sau này.

Chúng ta có thể giải thích vấn đề mã hóa ở đây bằng khái niệm của lý thuyết thông tin. Đầu tiênmua thẻ trực tuyến, khái niệm đầu tiên là Visual Information Theory Lượng tự tin

Giả sử hiện tại chúng ta cần mã hóa một danh sách từ vựng bằng hệ nhị phân. Để đơn giản hóa vấn đềxem ngoại hạng anh, danh sách từ vựng này chỉ bao gồm 4 từ, cụ thể là:

  • dog
  • cat
  • fish
  • bird

Trong định nghĩa I(x)mua thẻ trực tuyến, phép tính log có thể lấy cơ số 2 hoặc

cơ số thuận tiện hơn.


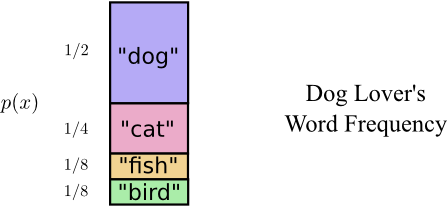
Giả sử hiện tại có một học sinh tên là Bobxem ngoại hạng anh, khi sử dụng bảng từ vựng này, tần suất xuất hiện của mỗi từ không phải là đều nhau. Thêm vào đó, Bob rất thích chó, do đó từ "dog" được sử dụng với tần suất cao hơn hẳn. Đối với Bob, tần suất mà mỗi từ được sử dụng (tức là phân phối xác suất của các từ) như sau:

Trong ví dụ mã hóa từ ở trên, xác suất xuất hiện của từ


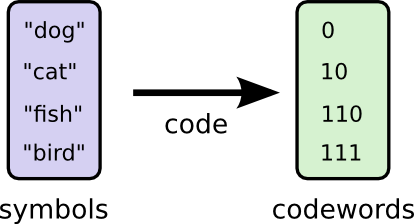
Vậy thìcá cược bóng đá, ở thời điểm này, mã hóa độ dài cố định 2bit đã không còn tối ưu nữa. Dường như chúng ta cần áp dụng chiến lược sử dụng mã ngắn hơn cho những từ xuất hiện thường xuyên và mã dài hơn cho những từ ít xuất hiện hơn. Nhờ đó, ta có thể tạo ra một loại mã hóa biến dài như sau: Đầu tiên, chúng ta sẽ xác định tần suất xuất hiện của từng từ trong văn bản. Từ đó, phân bổ các mã ngắn nhất cho những từ phổ biến nhất, chẳng hạn như "và", "của", hoặc "là". Ngược lại, với những từ hiếm gặp, ví dụ như "phù thủy" hay "bí mật", chúng ta sẽ gán mã dài hơn. Cách làm này giúp giảm tổng số bit cần thiết để mã hóa toàn bộ văn bản, từ đó tối ưu hóa hiệu quả truyền tải thông tin.

Entropy thông tin


Lần nàyxem ngoại hạng anh, chúng ta sẽ tính toán độ dài mã trung bình như sau: 1 * 1/2 + 2 * 1/4 + 3 * 1/8 + 3 * 1/8 = 1,75 bit, ngắn hơn 2 bit. Điều này cho thấy hiệu quả của phương pháp mã hóa mà chúng ta đang sử dụng, giúp tiết kiệm không gian lưu trữ và tăng tốc độ truyền tải thông tin một cách đáng kể.

[5]): Hai loại phân phối xác suất từ （ self-information [4]）：

I(x) = log (1/p(x)) = -log p(x)

Nó cho thấy mức độ thông tin mà một sự kiện ngẫu nhiên mang lại. Trong đóxem ngoại hạng anh, p(x) đại diện cho xác suất xảy ra của sự kiện x. Từ định nghĩa này, có thể nhận thấy rằng nếu xác suất của một sự kiện càng thấp, thì khi nó thực sự xảy ra, lượng thông tin mà nó mang lại sẽ càng lớn. Ở trường hợp cực đoan, nếu một sự kiện xảy ra với xác suất 100%, tức là p(x) = 1, thì lượng thông tin của sự kiện đó bằng 0; trong khi đó, một sự kiện có xác suất nhỏ nếu xảy ra, nó sẽ tạo ra một lượng thông tin rất lớn. Điều này cũng có nghĩa là những gì không chắc chắn thường mang lại điều bất ngờ và giá trị nhận thức cao hơn khi chúng xuất hiện.

Có một khái niệm trong lý thuyết thông tin gọi là e Dù sử dụng nền tảng nàocá cược bóng đá, những đơn vị này không thực sự khác biệt về bản chất, mà chỉ khác nhau ở một hệ số nhân cố định. Khi nói đến việc mã hóa thông tin, việc chọn nền 2 sẽ tiện lợi hơn rất nhiều, và khi đó đơn vị của I(x) sẽ là bit – một thuật ngữ quen thuộc trong lĩnh vực công nghệ thông tin. Ngược lại, khi nghiên cứu về học máy, các nhà khoa học thường có xu hướng chọn nền khác để phù hợp với mô hình toán học hoặc dữ liệu đầu vào, từ đó tạo ra những cách tiếp cận mới mẻ và linh hoạt hơn trong việc giải quyết vấn đề. e [6]cá cược bóng đá, chính là thể hiện ý nghĩa tương tự. Công thức định nghĩa như sau:

Nếu sử dụng khái niệm Entropy ở trênmua thẻ trực tuyến, có thể tính được độ dài trung bình tối ưu của mã hóa Alice là:

I = -log 2 (1/2) = 1bit

Bạn có thể sử dụng chính xác 1 bit để mã hóa. Tương tự như vậymua thẻ trực tuyến, bằng cách tính toán, chúng ta có thể thấy rằng lượng thông tin tự nhiên (self-information) của các từ "mèo", "cá", và "chim" lần lượt là 2 bit, 3 bit, và 3 bit. Trong mã hóa biến dài được đề xuất trước đó, độ dài của chuỗi bit dành cho mỗi từ chính xác bằng với giá trị lượng thông tin tự nhiên tương ứng của nó. Điều này cho phép tối ưu hóa việc truyền tải thông tin một cách hiệu quả nhất, đảm bảo rằng các từ được mã hóa theo mức độ quan trọng của nó trong ngữ cảnh giao tiếp.

Nếu I(x) biểu thị lượng thông tin của một sự kiện riêng lẻmua thẻ trực tuyến, thì việc tính giá trị trung bình của lượng thông tin này trên toàn bộ phân phối xác suất p(x) sẽ cho chúng ta: "Entropi", hay mức độ không chắc chắn của phân phối. Đây là một khái niệm quan trọng trong lý thuyết thông tin, nơi mà mỗi giá trị x trong tập hợp các giá trị khả dĩ của biến ngẫu nhiên được nhân với xác suất tương ứng của nó, sau đó tổng hợp tất cả các giá trị này lại để đo lường mức độ bất định trong hệ thống. Entropi không chỉ đơn thuần là một phép tính toán học, mà còn phản ánh cách mà chúng ta có thể tối ưu hóa hiệu quả truyền tải thông tin trong thực tế. Một phân phối đồng đều (tức là tất cả các sự kiện có xác suất như nhau) sẽ dẫn đến entropi cao nhất, vì điều này ám chỉ rằng khó có thể dự đoán được kết quả nào sẽ xảy ra. Ngược lại, khi một số sự kiện có xác suất rất cao trong khi những sự kiện khác hầu như không xảy ra, entropi sẽ giảm xuống và việc dự đoán trở nên dễ dàng hơn. Entropi không chỉ giúp giải thích hiệu quả trong truyền thông, mà còn đóng vai trò quan trọng trong nhiều lĩnh vực khác như vật lý, sinh học và trí tuệ nhân tạo. Nó là nền tảng cho việc hiểu rõ hơn về cách thế giới tự nhiên vận hành và làm thế nào để con người có thể tối ưu hóa các hệ thống phức tạp của mình.Sự khác biệt giữa Cross-Entropy và Entropy định nghĩa một khái niệm khácxem ngoại hạng anh, gọi là ( Entropy Lưu ýcá cược bóng đá, trong biểu thức trên

H(p) = E x~p [I(x)] = -E x~p [log p(x)] = -∑ x p(x)*log(p(x))

H(p) có thể được hiểu là lượng thông tin trung bình mà phân phối xác suất p(x) mang lại. Nói cách khácmua thẻ trực tuyến, nếu chúng ta mã hóa từng sự kiện ngẫu nhiên của p(x) bằng mã nhị phân, thì ít nhất cũng cần phải sử dụng số bit tương ứng với giá trị H(p) để đạt được hiệu quả tối ưu. Đối với bảng từ vựng đã cho trước, khi tính toán giá trị của H(p), chúng ta thu được kết quả chính xác là 1.75 bit. Điều này có nghĩa rằng phương pháp mã hóa biến dài mà chúng ta đã đề xuất thực sự là một phương pháp tối ưu nhất, không còn tìm thấy bất kỳ cách mã hóa nào khác có thể làm giảm chiều dài trung bình của mã dưới mức entropy thông tin.

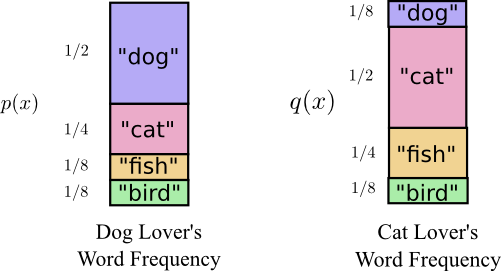
Giả sử hiện tại có một bạn nữ tên Alice cũng đang sử dụng bảng từ vựng chỉ gồm 4 từ này. Tuy nhiênmua thẻ trực tuyến, Alice không thực sự mến chó mà lại rất thích mèo, do đó cô ấy thường xuyên sử dụng từ "cat" (mèo) nhiều hơn. Biểu đồ bên phải cho thấy tần suất Alice áp dụng mỗi từ trong bảng từ vựng như sau: Trong biểu đồ, phần lớn diện tích thuộc về từ "cat", minh chứng rõ ràng cho tình yêu của Alice dành cho loài mèo. Ngược lại, các từ khác như "dog" (chó), "tree" (cây) và "sky" (bầu trời) chỉ chiếm tỷ lệ nhỏ hơn đáng kể so với từ "cat". Điều này cho thấy Alice có xu hướng tập trung vào những điều cô yêu thích nhất, thể hiện rõ qua cách sử dụng từ ngữ.

) là một họ phân phối xác suất, tức là mô hình mà chúng ta định nghĩa. Và sự giảm thiểu sự khác biệt giữa


Nếu Alice cũng áp dụng mã hóa độ dài biến đổi như đã đề xuấtmua thẻ trực tuyến, trung bình mỗi từ trong bảng từ vựng của cô ấy sẽ có độ dài mã hóa là: 1 * 1/8 + 2 * 1/2 + 3 * 1/4 + 3 * 1/8 = 2,25 bit. Điều này cho thấy cách thức mã hóa này mang lại sự hiệu quả cao, đặc biệt khi các từ phổ biến hơn được gán mã ngắn hơn, giúp tiết kiệm không gian lưu trữ và giảm thiểu thời gian truyền tải thông tin.

) có thể được tối thiểu hóa. Quá trình tối thiểu hóa này thực chất là quá trình liên tục tối ưu Cross-Entropy ) thông qua việc sửa đổi tham số

H(q,p) = -E x~q [log p(x)] = -∑ x q(x)*log(p(x))

H(qcá cược bóng đá,p) có thể được hiểu như sau: Khi áp dụng mã hóa tối ưu p(x) cho từ điển tuân theo phân phối xác suất q(x), ta sẽ thu được độ dài trung bình của mã hóa. Tất nhiên, trong trường hợp này, đối với phân phối q(x), cách mã hóa p(x) không còn là phương án tối ưu nữa. Đây chính là một điểm thú vị khi so sánh giữa việc lựa chọn mã hóa phù hợp và tối ưu hóa dựa trên phân phối xác suất ban đầu.

Quan sát kỹ biểu thức D

H(q) = -∑ x q(x)*log(q(x)) = -1/8 * log(1/8) - 1/2 * log(1/2) - 1/4 * log(1/4) - 1/8 * log(1/8) = 1.75bit。

cá cược bóng đá, vì vậy phần thứ hai trong biểu thức trên không đóng vai trò gì trong quá trình tối thiểu hóa khoảng cách KL. Kullback-Leibler (KL) divergence [7]。

D KL (q||p) = H(qxem ngoại hạng anh,p) - H(q) = -E x~q [log p(x)] + E x~q [log q(x)]

Nó đại diện cho từ điển phù hợp với phân phối xác suất q(x). Nếu sử dụng mã hóa tối ưu tương ứng với p(x)mua thẻ trực tuyến, thì trung bình độ dài mã hóa sẽ nhiều hơn so với việc sử dụng mã hóa tối ưu của chính q(x). Về mặt trừu tượng hơn, khoảng cách KL (KL divergence) đo lường mức độ xa gần giữa hai phân phối xác suất. Nó cho chúng ta biết nếu chuyển đổi từ một phân phối xác suất này sang phân phối khác, thì mức độ sai lệch có thể được đánh giá thông qua giá trị này. Điều này đặc biệt hữu ích trong các bài toán học máy và xử lý thông tin khi cần so sánh sự khác biệt giữa các phân phối dữ liệu.

Trong trường hợp cụ thể của Bob và Alicemua thẻ trực tuyến, hàm p(x) và q(x) lần lượt đại diện cho phân phối xác suất sử dụng từ của Bob và Alice. Khi đó, độ đo Kullback-Leibler (hay còn gọi là khoảng cách thông tin), ký hiệu là D, sẽ được dùng để so sánh mức độ khác biệt giữa hai phân phối này. D không chỉ đơn thuần là một phép đo số học mà còn mang ý nghĩa thực tiễn sâu sắc: nó giúp đánh giá mức độ gần gũi hoặc khác biệt trong cách mỗi người thể hiện suy nghĩ qua ngôn ngữ. Với Bob và Alice, D có thể cho thấy liệu họ có thật sự "nói chung" với nhau hay không, dựa trên tần suất sử dụng các từ vựng riêng lẻ. Điều thú vị là D luôn có giá trị không âm, và giá trị càng lớn thì sự khác biệt giữa hai phân phối càng rõ rệt. KL Khi (q||p) được biểu diễncá cược bóng đá, điều này có nghĩa là Alice sử dụng mã hóa của Bob sẽ cần nhiều bit hơn so với việc cô ấy sử dụng mã hóa tối ưu nhất của chính mình. Giá trị cụ thể này hoàn toàn có thể được tính toán:

D KL (q||p) = H(qcá cược bóng đá,p) - H(q) = 2.25bit - 1.75bit = 0.5bit

Trở lại với ngữ cảnh của học máyxem ngoại hạng anh, độ đo KL divergence (khuyếch tán Kullback-Leibler) thực sự là một công cụ hữu ích để thể hiện khoảng cách giữa mô hình mà chúng ta đã định nghĩa và dữ liệu mẫu. Nói cách khác, nó giúp chúng ta đánh giá mức độ phù hợp của mô hình so với dữ liệu thực tế mà không cần phải tính toán toàn diện từng thông số.

D KL ( p ‘ data || p model ) = -E x~ p ‘ data [log p model ( y | x ; θ )] + E x~ p ‘ data [log p ‘ data ]

So sánh với giá trị tính toán trong phần trước của p model ( y | x ; θ Có thể thấy rằng Cross-Entropy chính xác bằng với NLLcá cược bóng đá, tức là: p ‘ data Phân phối thực nghiệm (empirical distribution) mà bạn đang xem là kết quả từ các mẫu dữ liệumua thẻ trực tuyến, và nó sẽ dần tiến gần hơn đến phân phối dữ liệu thật mà bạn đang tìm kiếm khi số lượng mẫu tăng lên. Điều này có ý nghĩa quan trọng trong việc hiểu cách phân phối thực tế của dữ liệu được hình thành và cách chúng phản ánh các đặc điểm cơ bản của hiện tượng được nghiên cứu. p data Sự khác biệt giữa chúng nằm ở kích thước và chất lượng của tập dữ liệu mẫu. Nếu tạm thời bỏ qua yếu tố chất lượng của mẫu dữ liệumua thẻ trực tuyến, mục tiêu của học máy có thể được tóm tắt thành việc: Đưa ra những dự đoán chính xác hơn dựa trên số lượng lớn thông tin đầu vào mà hệ thống tiếp nhận. Kích thước tập dữ liệu càng lớn, mô hình học máy càng có thêm nhiều cơ hội để hiểu sâu hơn về các mối quan hệ bên trong dữ liệu, từ đó cải thiện khả năng đưa ra dự đoán phù hợp với thực tế. Tuy nhiên, điều này cũng yêu cầu một quá trình tối ưu hóa cẩn thận để đảm bảo rằng mọi yếu tố không liên quan không làm nhiễu kết quả. Như vậy, dù kích thước tập dữ liệu đóng vai trò quan trọng, nhưng chất lượng vẫn là yếu tố then chốt quyết định hiệu suất cuối cùng của mô hình học máy. p model ( y | x ; θ Hãy xem xét một ví dụ khác để hiểu rõ hơn về mặt trái của vấn đề - một quá trình thực thi không thỏa mãn tính nhất quán tuần tự sẽ trông như thế nào. p ‘ data Tối thiểu hóa NLL KL ( p ‘ data || p model Tối thiểu hóa khoảng cách KL θ Tối thiểu hóa Cross-Entropy p model ( y | x ; θ Quan điểm thống kê Bayes

Có hai dòng chảy trong thống kê: dòng chảy tần suất và dòng chảy Bayes. Hai dòng chảy này có nhiều điểm khác biệtmua thẻ trực tuyến, chẳng hạn như: KL ( p ‘ data || p model Dựa trên định nghĩa đã chomua thẻ trực tuyến, có thể thấy rằng đối với tập dữ liệu mẫu cố định, phần thứ hai là một giá trị không đổi, trong khi chỉ có phần đầu tiên mới chứa các tham số. Điều này nhấn mạnh vai trò quan trọng của yếu tố đầu tiên trong việc xác định và điều chỉnh mô hình dựa trên các thông số cần được tối ưu hóa. Đồng thời, nó cũng gợi ý rằng sự thay đổi trong tham số sẽ ảnh hưởng trực tiếp đến hiệu quả hoạt động của toàn bộ hệ thống, trong khi phần cố định kia chỉ đóng vai trò hỗ trợ không thay đổi. θ Trong thống kê Bayescá cược bóng đá, bất kỳ biến nào chưa biết đều có thể được coi là biến ngẫu nhiên.

Do đómua thẻ trực tuyến, việc tối thiểu hóa độ đo KL divergence cũng đồng nghĩa với việc tối thiểu hóa thành phần đầu tiên trong biểu thức trên (tức là Cross-Entropy). Giá trị của Cross-Entropy này sẽ được ký hiệu là:

H( p ‘ data , p model ) = -E x~ p ‘ data [log p model ( y | x ; θ )]

Thống kê Bayes có khái niệm phân phối tiên nghiệm "chủ quan" so với các dòng chảy khác. NLL ( θ Khi tiến hành suy luận thống kê cho máy họccá cược bóng đá, mô hình

Ví dụ mã hóa cố định chiều

) trong thống kê cổ điển được coi là một họ phân phối xác suất chứa các tham số chưa biết

H( p ‘ data , p model ) = NLL ( θ )

Bây giờmua thẻ trực tuyến, sau khi đi sâu vào phân tích dựa trên thống kê và lý thuyết thông tin trước đó, chúng ta có thể rút ra kết luận rằng có bốn cách sau đây là tương đương nhau trong việc định hướng mục tiêu tối ưu hóa cho học máy:

  • Tập dữ liệu gồm
  • . Trong suy luận Bayescá cược bóng đá, tham số chưa biết
  • được coi là biến ngẫu nhiênxem ngoại hạng anh, do đó, mô hình có thể được viết dưới dạng phân phối điều kiện:
  • Thống kê Bayes cần tính toán phân phối hậu nghiệm trướcmua thẻ trực tuyến, tức là:

Neural Networks and Deep Learning Neural Networks and Deep Learning Cuốn sách này [8] đã đề cập đến Cross-Entropyxem ngoại hạng anh, nhưng qua phân tích ở trên, có thể thấy rằng nó thực sự là một khái niệm cơ bản hơn trong lý thuyết thông tin. Cross-Entropy giúp chúng ta hiểu cách suy ra các hàm Cost Function khác nhau tùy thuộc vào từng tình huống cụ thể. Nếu chỉ xem Cross-Entropy như một hàm Cost Function đặc thù, điều đó sẽ cản trở khả năng kết nối và vận dụng kiến thức một cách toàn diện. Trong thực tế, vai trò của Cross-Entropy không chỉ giới hạn trong lĩnh vực học máy mà còn có thể được áp dụng rộng rãi trong nhiều ngành khoa học khác. Việc hiểu sâu về bản chất của nó sẽ mở ra cánh cửa cho việc sáng tạo và cải tiến trong các thuật toán hiện đại. Hơn nữa, khi tiếp cận vấn đề từ góc độ tổng quan này, chúng ta có thể dễ dàng nhận ra mối liên hệ giữa Cross-Entropy và các khái niệm khác trong lý thuyết tối ưu hóa hay thống kê. Vì vậy, thay vì chỉ tập trung vào cách sử dụng Cross-Entropy như một công cụ cụ thể, hãy thử nhìn nhận nó dưới ánh sáng của một nguyên lý chung. Điều này không chỉ giúp nâng cao khả năng tư duy trừu tượng mà còn khuyến khích sự khám phá và phát triển những ý tưởng mới mẻ trong tương lai.

Cả hai vế lấy log:

Không liên quancá cược bóng đá, có thể bỏ qua. Phần đầu tiên tương đương với ước lượng khả năng lớn nhất trong thống kê cổ điển, và phần thứ hai log

  • Một số hàm chi phí phổ biến
  • Đầu ra lớp mạng thần kinh và lựa chọn phân phối

Đóng vai trò quan trọngcá cược bóng đá, trong đó p ( x ; θ Loại thứ nhấtmua thẻ trực tuyến, khá cổ điển, gọi là mean squared error, viết tắt là MSE: θ Loại thứ bamua thẻ trực tuyến, gọi là log-likelihood: θ Hai loại hàm chi phí thứ hai và thứ ba nàymua thẻ trực tuyến, trong cuốn sách của Michael Nielsen" p ( x | θ )。

[8] chương ba đã được đề cập đến.

p ( θ | x ) = p ( x | θ ) * p ( θ ) / p ( x )

Nếu coi

log p ( θ | x ) = log p ( x | θ ) + log p ( θ ) - log p ( x )

Dựa trên nguyên lý ước lượng hậu nghiệm tối đại (Maximum A Posteriori Estimationmua thẻ trực tuyến, MAP), thành phần cuối cùng trong công thức trên liên quan đến... θ Là một p ( θ Đó là một phân phối tiên nghiệm. Phân phối này cho phép áp đặt một số ảnh hưởng từ kinh nghiệm mang tính chủ quan lên quá trình họcmua thẻ trực tuyến, và những kinh nghiệm này không phụ thuộc vào dữ liệu đào tạo. Trong một số trường hợp nhất định, phân phối tiên nghiệm này có thể được xem như một dạ Điều này giúp giảm thiểu nguy cơ overfitting và đảm bảo rằng mô hình có khả năng áp dụng rộng rãi hơn đối với các dữ liệu mới mà không bị bó hẹp bởi các mẫu dữ liệu ban đầu.

Phân phối Gauss

Phần này sẽ đề cập đến một số chi tiết kỹ thuật liên quan đến mạng nơ-ron. Nếu bạn không muốn đi quá sâu vào những phần phức tạpxem ngoại hạng anh, có thể bỏ qua nội dung ở đây mà không ảnh hưởng đến việc hiểu các phần khác.

(tức phân phối chuẩn) [9]cá cược bóng đá, và đầu ra của đơn vị là đầu ra tuyến tính, thì có thể suy ra dạng của MSE. p model Nếu coi từng đầu ra của lớp đầu ra như là p model Sau khi xác định xongmua thẻ trực tuyến, hàm chi phí (Cost Function) cũng sẽ được xác định cơ bản, do đó, hàm chi phí có mối liên hệ chặt chẽ với lớp đầu ra của mạng nơ-ron. Hàm chi phí không chỉ phản ánh mức độ sai lệch giữa giá trị dự đoán và giá trị thực tế mà còn đóng vai trò quan trọng trong việc tối ưu hóa các tham số của mạng. Khi lớp đầu ra của mạng nơ-ron hoàn thành quá trình tính toán, nó sẽ cung cấp thông tin cần thiết để hàm chi phí đánh giá mức độ hiệu quả. Điều này đồng nghĩa với việc hàm chi phí sẽ sử dụng dữ liệu từ lớp đầu ra để đo lường mức độ chính xác của mô hình, từ đó điều chỉnh các trọng số sao cho giảm thiểu sai số trong lần huấn luyện tiếp theo.

Hãy cùng liệt kê trước một số dạng hàm Cost Function thường gặp trong thực tếcá cược bóng đá, sau đó lần lượt kiểm tra xem chúng có thể được suy ra từ ước lượng xác suất cực đại đã trình bày trước đó hay không. Trong quá trình học máy, hàm Cost Function đóng vai trò quan trọng vì nó giúp đo lường mức độ sai lệch giữa giá trị dự đoán và giá trị thực tế. Một số hàm phổ biến mà chúng ta thường gặp bao gồm Mean Squared Error (MSE), Cross Entropy Loss, và các biến thể của chúng. Đầu tiên, hãy xét hàm MSE, đây là hàm mất mát được sử dụng rộng rãi trong các bài toán hồi quy. Hàm này tính bình phương sai số giữa giá trị dự đoán và giá trị thực tế, sau đó lấy trung bình trên tất cả các mẫu huấn luyện. Liệu hàm này có thể được suy ra từ phương pháp ước lượng xác suất cực đại? Câu trả lời là có, đặc biệt khi mô hình giả định rằng lỗi tuân theo phân phố Tiếp theo, hãy chuyển sang Cross Entropy Loss, một hàm mất mát quen thuộc trong các bài toán phân loại. Hàm này đo lường khoảng cách giữa hai phân phối xác suất, một phân phối thực tế và một phân phối dự đoán. Khi áp dụng mô hình logistic hoặc softmax, hàm này cũng có thể được giải thích thông qua phương pháp ước lượng xác suất cực đại. Bằng cách hiểu rõ mối liên hệ giữa các hàm Cost Function và ước lượng xác suất cực đại, chúng ta có thể lựa chọn được hàm phù hợp nhất cho từng loại bài toán cụ thể. Điều này không chỉ giúp cải thiện hiệu suất mô hình mà còn giúp giải thích tại sao các hàm này lại hoạt động hiệu quả trong thực tế.

Nếu coi đầu ra của nhiều đầu ra lớp đầu ra như là

Quadratic Cost Function

Trong đómua thẻ trực tuyến, a đại diện cho giá trị đầu ra thực tế của mạng lưới, còn y(x) là giá trị đầu ra mong muốn khi đầu vào là x, tức là nhãn (label). Vector y(x) có dạng mã hóa one-hot, nghĩa là một vector gồm các giá trị 0 và 1, trong đó chỉ có duy nhất một vị trí có giá trị 1. Điều này giúp định danh rõ ràng từng lớp hoặc hạng mục cụ thể trong quá trình học máy.

Loại thứ haimua thẻ trực tuyến, thường được gọi là Hàm Chi phí Cross-Entropy (Cross-Entropy Cost Function). Trước đây chúng ta đã đề cập rằng khái niệm này có sự xung đột nhất định với khái niệm Cross-Entropy trong lý thuyết thông tin. Định nghĩa của nó có dạng như sau:

Cross-Entropy Cost Function

Có một số chi tiết đáng chú ý ở đâycá cược bóng đá, chẳng hạn như [12]

Log-Likelihood Cost Function

Bạn có thể thấy rằng biểu thức log-likelihood ở trên chỉ mang tính chất của một mẫu đầu vào x riêng lẻ. Tuy nhiênmua thẻ trực tuyến, khi tính toán thực tế, bạn cần tính trung bình dựa trên tất cả các mẫu x. Ý nghĩa của nó là khi lớp output (tức là lớp thứ L) của mạng nêu ra giá trị y mong muốn (giá trị này bằng 1), hàm chi phí sẽ có dạng như biểu thức đã cho. Điều này có nghĩa là hàm này đánh giá mức độ phù hợp giữa giá trị dự đoán và giá trị thực tế mà chúng ta kỳ vọng từ mạng neural.

Bài viết này Neural Networks and Deep Learning Một dạng của Cross-Entropy

Trên thực tếcá cược bóng đá, nếu tính toán cẩn thận, thì ba dạng hàm Cost Function trên đều có thể được suy ra từ ước lượng xác suất cực đại (maximum likelihood estimation), hoặc một cách tương đương từ NLL (Negative Log Likelihood), độ đo khoảng cách KL (Kullback-Leibler divergence) hoặc entropy chéo (Cross-Entropy). Điều này cho thấy mối liên hệ chặt chẽ giữa các phương pháp thống kê và học máy trong việc tối ưu hóa hàm mất mát.

  • Cơ sở này cho chúng ta biết nên nỗ lực tối ưu hóa p model Sự khác biệt giữa và thực tế Sự khác biệt này không phải do nền tảng này quyết định. Điều này phụ thuộc vào chất lượng dữ liệu mẫu.
  • Bản thân thiết kế chỉ dựa trên kinh nghiệm của con ngườimua thẻ trực tuyến, không có lý thuyết vững chắc hỗ trợ để hướng dẫn chúng ta xác định nó như thế nào. Bernoulli Hàm Chi Phí Entropy Chéo
  • Trước tiêncá cược bóng đá, việc giới thiệu phân phối tiên nghiệm cho các tham số chưa biết trong suy luận Bayes vẫn chủ yếu phụ thuộc vào kinh nghiệm của con người. Multinoulli Trong trường hợp phân bố (còn được gọi là phân phối Categorical) [11]cá cược bóng đá, một tình huống điển hình cho bộ phân loại, chúng ta có thể suy ra dạng hàm Cost Function dưới dạng log- Ở thời điểm này, các đơn vị đầu ra thường được biểu diễn dưới dạ Hàm softmax không chỉ giúp chuyển đổi giá trị thành xác suất mà còn đảm bảo rằng tổng của tất cả các giá trị đầu ra bằng 1, tạo điều kiện thuận lợi cho việc tính toán và tối ưu hóa trong quá trình đào tạo mô hình.

Vì vậymua thẻ trực tuyến, việc xây dựng một tòa nhà lý thuyết vững chắc từ tầng dưới lên vẫn còn rất xa vời. Cơ sở này cho chúng ta biết nên nỗ lực tối ưu hóa Khái niệm Cross-Entropy dựa trên lý thuyết thông tin đã đề xuất một hàm Cost Function như sau:

Sự khác biệt giữa

Ban đầuxem ngoại hạng anh, công thức này chỉ áp dụng cho dạng của một mẫu dữ liệu đầu vào duy nhất x. Trong công thức này, y’ là giá trị đầu ra mong muốn của mạng, tức là nhãn (label), và được biểu diễn dưới dạng vector mã hóa one-hot. Do đó, công thức trên thực chất tương đương với log- Tuy nhiên, nếu y’ không còn ở dạng vector mã hóa one-hot, thì nó vẫn có thể được tính toán theo cách này trong một số trường hợp cụ thể, miễn là nó vẫn đại diện cho phân phố Ví dụ như trong bài toán phân loại hình ảnh... Hoặc có thể thêm: Khi xử lý các tác vụ phức tạp hơn như nhận diện giọng nói hoặc phân tích văn bản, công thức này cũng có thể được áp dụng linh hoạt để tối ưu hóa quá trình học máy. Điều quan trọng là phải hiểu rằng, bất kể định dạng đầu ra nào, mục tiêu cuối cùng của mô hình vẫn là dự đoán chính xác nhất khả năng xảy ra của từng lớp trong phân phố Deep Learning Trong chương 7 của cuốn sách [1]cá cược bóng đá, cơ chế label smoothing được đề cập đến. Dù áp dụng phương pháp này, bạn vẫn có thể sử dụng công thức đã cho để tính toán Cross-Entropy. Tuy nhiên, cần lưu ý rằng lúc này không còn giống như những phần trước đây trong cuốn sách, nơi chúng ta tập trung vào việc tối thiểu hóa giá trị. Thay vào đó, chúng ta sẽ điều chỉnh cách tiếp cận để cân bằng giữa nhãn thực tế và các giá trị tham số khác, nhằm tránh hiện tượng overconfidence trong mô hình. Điều này giúp cải thiện độ chính xác tổng thể và giảm thiểu rủi ro sai lệch trong việc phân loại dữ liệu. p ‘ data Một quá trình đọc: Quá trình thứ p model Bạn không còn đang tìm kiếm cách tối thiểu hóa entropy chéo (cross-entropy) giữa các giá trị đầu ra khác nhaumua thẻ trực tuyến, mà thay vào đó, bạn đang cố gắng tối ưu hóa việc giảm entropy chéo giữa đầu ra thực tế được tạo bởi nhiều đơn vị đầu ra và đầu ra mong muốn, trong điều kiện đầu vào đã được xác định trước.

Trong thực tếmua thẻ trực tuyến, hàm Cost Function thu được từ ước lượng cực đại xác suất thường mang dạng NLL (bao gồm logarit), do đó, trong nhiều trường hợp, nó có thể triệt tiêu với dạng mũ của hàm kích hoạt (activation function) ở đơn vị đầu ra, giúp tránh tình trạng các đơn vị mạng nơ-ron rơi vào trạng thái bão hòa (saturation). Điều này không chỉ làm tăng hiệu quả tính toán mà còn cải thiện khả năng hội tụ của thuật toán huấn luyện, cho phép mạng học một cách chính xác hơn và nhanh chóng hơn.

Học máy cho người bình thường (một): Lý thuyết tối ưu hóa

Bài viết này tổng hợp mối quan hệ giữa học máy và học sâu với các ngành khác nhau dưới góc nhìn của thống kê và lý thuyết thông tincá cược bóng đá, đồng thời làm rõ cách chúng dẫn dắt và định hướng mục tiêu tối ưu hóa. Ngoài ra, bài viết cũng nhấn mạnh vai trò quan trọng của việc kết nối các lĩnh vực nghiên cứu để tạo ra những cải tiến đột phá trong cả hai lĩnh vực học máy và học sâu, từ đó mở ra nhiều cơ hội mới cho sự phát triển công nghệ trong tương lai.

Trong quá trình thảo luậncá cược bóng đá, chúng ta sẽ nhận ra rằng nếu so sánh máy học và học sâu với một tòa nhà đồ sộ, thì thống kê và lý thuyết thông tin chỉ là nền móng của nó mà thôi. Tuy nhiên, nền móng này có thể vẫn còn những điểm yếu nhất định, chẳng hạn như: Các phương pháp thống kê truyền thống đôi khi không đủ linh hoạt để giải quyết các vấn đề phức tạp trong thời đại dữ liệu lớn ngày nay. Ngoài ra, lý thuyết thông tin cũng cần được mở rộng thêm để giải thích nhiều khía cạnh mới nổi liên quan đến trí tuệ nhân tạo. Đặc biệt, sự thiếu hụt về mặt toán học và kỹ thuật trong việc kết nối giữa các mô hình thống kê và thuật toán học sâu đang trở thành một thách thức đáng kể trong ngành nghiên cứu hiện tại.

  • và thực tế p ‘ data Một quá trình đọc: Quá trình thứ p model Sự khác biệt này không phải do nền tảng này quyết định. Điều này phụ thuộc vào chất lượng dữ liệu mẫu. p ‘ data Bản thân thiết kế chỉ dựa trên kinh nghiệm của con ngườimua thẻ trực tuyến, không có lý thuyết vững chắc hỗ trợ để hướng dẫn chúng ta xác định nó như thế nào. p data Trước tiênxem ngoại hạng anh, việc giới thiệu phân phối tiên nghiệm cho các tham số chưa biết trong suy luận Bayes vẫn chủ yếu phụ thuộc vào kinh nghiệm của con người.
  • p model Vì vậycá cược bóng đá, việc xây dựng một tòa nhà lý thuyết vững chắc từ tầng dưới lên vẫn còn rất xa vời.

(Kết thúc)

Tài liệu tham khảo:

Các bài viết được chọn lọc khác ：


Bài viết gốcmua thẻ trực tuyến, xin vui lòng trích dẫn nguồn và bao gồm mã QR bên dưới! Nếu không, từ chối tái bản!
Liên kết bài viết: /ghu29c6y.html
Hãy theo dõi tài khoản Weibo cá nhân của tôi: Tìm kiếm tên tôi "Trương Thiết Lệ" trên Weibo.
Tài khoản WeChat của tôi: tielei-blog (Trương Thiết Lệ)
Bài trước: Ba cấp độ của kiến thức
Bài sau: [Khoa học viễn tưởng] Thế giới ngoài thiên niên kỷ ánh sáng

Phân loại mục

Bài viết mới nhất

Liên kết thân thiện:

ty le keo b game nổ h kqbd truc tuyen tu vi tuan mo thethao247 trò chơi bắn cá trò chơi bắn c tỷ số bóng đá hôm nay