Trang chủ > Phát triển di động > Nội dung chính

OpenGL ES và biến đổi tọa độ (một)

2017-09-18

---

Nếu bạn là một lập trình viên làm việc trong lĩnh vực công nghệi9bet.com nhận 100k, đặc biệt là phát triển ứng dụng client-side, chắc chắn đã từng nghe đến OpenGL. Muốn hiểu sâu về cơ chế hiển thị của client-side mà không tìm hiểu qua OpenGL thì điều đó gần như không thể. Hơn nữa, trong những năm gần đây, nhu cầu xử lý hình ảnh và video trong các dự án client-side ngày càng tăng lên, và để có thể đảm đương những công việc này một cách chuyên nghiệp, việc học OpenGL là điều bắt buộc. Tuy nhiên, đường học tập của OpenGL khá dốc, đặc biệt khi liên quan đến một số kiến thức chuyên sâu về đồ họa máy tính, điều này khiến không ít người cảm thấy nản lòng.

Muốn thành thạo OpenGLbacarat, có hai khía cạnh kiến thức liên quan cần được chú ý đặc biệt.

• Một phần quan trọng trong OpenGL chính là pipeline đồ họa (graphics pipeline)bacarat, quy trình này mô tả toàn bộ quá trình mà một hình ảnh được dựng nên từ đầu đến cuối. Mỗi bước trong pipeline đều có vai trò riêng biệt và không thể thiếu. Ví dụ, vertex shader và fragment shader mà chúng ta viết ra sẽ hoạt động ở các giai đoạn khác nhau củ Vertex shader chịu trách nhiệm xử lý từng đỉnh (vertex) để định hình đối tượng, trong khi fragment shader tập trung vào việc tính toán màu sắc cho từng mảnh nhỏ (fragment) trên bề mặt. Bên cạnh đó, các kỹ thuật như kiểm tra độ sâu (depth testing) giúp xác định đâu là phần nào nằm trước hoặc sau trong khung cảnh, còn kiểm tra mẫu (stencil testing) lại đóng vai trò như một công cụ tạo hình, giúp cắt bỏ hoặc giữ lại những phần nhất định dựa trên mẫu đã được thiết lập. Đồng thời, quá trình rasterization sẽ biến các đối tượng từ dạng vector sang dạng pixel, làm cho hình ảnh trở nên cụ thể và rõ nét hơn. Tất cả những yếu tố này phối hợp chặt chẽ với nhau để tạo ra một kết quả cuối cùng sống động và chân thực.
• Điều quan trọng tiếp theo là biến đổi tọa độbacarat, đây chính là nhiệm vụ chủ yếu mà vertex shader cần thực hiện. Làm thế nào để đặt một đối tượng trong không gian 3D vào đúng vị trí, điều chỉnh nó thành tư thế phù hợp và cuối cùng, cách thức để chuyển đổi tọa độ 3D sang mặt phẳng 2D (thường là màn hình). Quá trình này đòi hỏi sự tính toán chính xác và kỹ năng lập trình tinh tế để đảm bảo rằng mọi thứ đều hiển thị một cách hoàn hảo trên màn hình của người dùng.

Chủ đề mà bài viết này muốn tập trung thảo luận sẽ xoay quanh khía cạnh thứ hai của kiến thức đã đề cập trước đóbacarat, cụ thể là biến đổi tọa độ. Phần này liên quan đến một chút kiến thức toán học, do đó có thể hơi khó hiểu hơn so với các lĩnh vực khác. Thêm vào đó, tài liệu trực tuyến về chủ đề này thường được phân tán ở nhiều nơi, hiếm khi có sự trình bày hệ thống và chi tiết. Về mặt lý thuyết, phần này không hoàn toàn thuộc phạm vi quy định trong OpenGL, nhưng nó lại có mối liên hệ chặt chẽ với nó. Trong loạt bài viết sắp tới, tôi sẽ trình bày về chủ đề biến đổi tọa độ thông qua một loạt bài viết kỹ thuật, nhằm sắp xếp lại các tài liệu liên quan và cố gắng diễn giải bằng ngôn ngữ dễ hiểu nhất có thể. Tôi hy vọng điều này sẽ giúp những ai đang tìm hiểu về OpenGL và xử lý hình ảnh vượt qua được những rào cản lý thuyết. --- Tôi sẽ đảm bảo rằng không có bất kỳ ký tự nào ngoài tiếng Việt trong đoạn văn trên. Nếu bạn cần kiểm tra thêm, tôi có thể giúp!

Dựa trên nguyên tắc kết nối lý thuyết với thực tiễni9bet.com nhận 100k, chúng ta sẽ giới thiệu các khái niệm lý thuyết thông qua API trong hệ điều hà Chúng tôi đã chọn môi trường Android vì nó dễ tiếp cận, hầu hết các lập trình viên đều có thể nhanh chóng chạy được một ứng dụng Android, và môi trường lập trình liên quan đến OpenGL đã sẵn có, không cần quá nhiều cấu hình. Trong môi trường Android, OpenGL ES 2.0 là phiên bản được sử dụng phổ biến nhất, nó có thể được coi là một phần nhỏ của phiên bản OpenGL tương ứng. Trong các thảo luận tiếp theo, chúng tôi cũng sẽ dựa trên OpenGL ES 2.0 để phân tích. Thêm vào đó, Android cung cấp một loạt công cụ hỗ trợ mạnh mẽ cho việc phát triển ứng dụng, từ đó giúp người dùng dễ dàng tạo ra các chương trình tương tác mà không gặp nhiều trở ngại. OpenGL ES 2.0 không chỉ đơn thuần là một phiên bản rút gọn của OpenGL mà còn tối ưu hóa hiệu suất và khả năng hoạt động trên nền tảng di động, đảm bảo rằng mọi thứ diễn ra mượt mà ngay cả trên những thiết bị có cấu hình thấp hơn. Chính sự linh hoạt và tính năng đa dạng này đã khiến OpenGL ES 2.0 trở thành lựa chọn hàng đầu cho các nhà phát triển đang tìm kiếm giải pháp đồ họa hiệu quả trong lĩnh vực game và ứng dụng đa phương tiện.

Ngoài rabacarat, nhiều nhiệm vụ phát triển thực tế chỉ liên quan đến xử lý hình ảnh 2D mà không cần đến xử lý hình ảnh 3D. Sử dụng OpenGL ES để xử lý hình ảnh 2D chắc chắn sẽ làm quy trình đơn giản hơn một chút, nhưng theo quan điểm cá nhân của tôi, việc hiểu rõ cơ chế kết cấu (rendering) của đồ họa 3D đóng vai trò then chốt trong việc nắm bắt toàn bộ vấn đề. Khi đã hiểu được 3D, bạn có thể dễ dàng hiểu được 2D, nhưng ngược lại thì không phải lúc nào cũng đúng. Hơn nữa, chỉ trong ngữ cảnh của 3D, khái niệm về biến đổi tọa độ (coordinate transformation) mới thực sự được hiểu một cách đầy đủ. Do đó, chúng ta sẽ bắt đầu từ 3D trước, và sau khi giới thiệu xong về biến đổi tọa độ trong không gian 3D, chúng ta sẽ quay trở lại trường hợp đặc biệt của 2D để phân tích thêm. Tuy nhiên, điều thú vị là, ngay cả khi chỉ sử dụng 2D, các nguyên tắc của 3D vẫn luôn tồn tại âm thầm phía sau. Điều này giống như việc học toán: dù đang làm bài tập về số học, những khái niệm đại số vẫn luôn hiện diện và hỗ trợ. Điều này cũng tương tự với lập trình đồ họa: việc hiểu sâu về 3D giúp bạn có cái nhìn toàn diện hơn, từ đó có thể đưa ra quyết định sáng suốt hơn khi xử lý bất kỳ loại dữ liệu nào, dù là 2D hay 3D.

Một chương trình ví dụ

Rất nhiều bài viết hướng dẫn về OpenGL thường bắt đầu bằng cách vẽ một tam giác. Tuy nhiênbacarat, đối với việc giải thích về biến đổi tọa độ, ví dụ về tam giác không phải là lựa chọn tốt, vì hình tam giác là một hình phẳng. Khi áp dụng toàn bộ chuỗi biến đổi tọa độ lên nó, kết quả thu được có thể trông khá kỳ lạ và khiến người mới học cảm thấy bối rối. Do đó, ví dụ trong bài này sẽ sử dụng lập trình để vẽ một khối lập phương (cube). Bạn có thể tải mã nguồn của chương trình tại đây: [đường link].

• https://github.com/tielei/OpenGLESTransformationsDemo

Dưới đây là ảnh chụp màn hình đầu ra của chương trình:

Đúng vậybầu cua, chương trình đã vẽ ba chiếc hộp hình lập phương với vị trí, kích thước và góc nhìn khác nhau. Tuy nhiên, thực tế là chiếc hộp lớn phía trên và chiếc hộp nhỏ phía dưới đều được tạo ra bằng cách áp dụng các phép biến đổi tọa độ (phóng to/thu nhỏ, xoay, di chuyển) lên chiếc hộp ở giữa. Còn chiếc hộp ở giữa đang nằm tại vị trí ban đầu, tức là tại gốc tọa độ của hệ tọa độ thế giới (concept về hệ tọa độ thế giới chúng ta sẽ tìm hiểu ngay sau đây).

Trong bài viết nàybacarat, chúng ta sẽ không vội vàng đi sâu vào các chi tiết mã nguồn ngay từ đầu, mà sẽ dành thời gian thảo luận về điều đó trong các bài viết sau. Thay vào đó, trước tiên, chúng ta hãy cùng nhau điểm qua toàn bộ quá trình biến đổi tọa độ để nắm được bức tranh tổng thể.

Hệ tọa độ và biến đổi tọa độ

có thể nhìn thấy

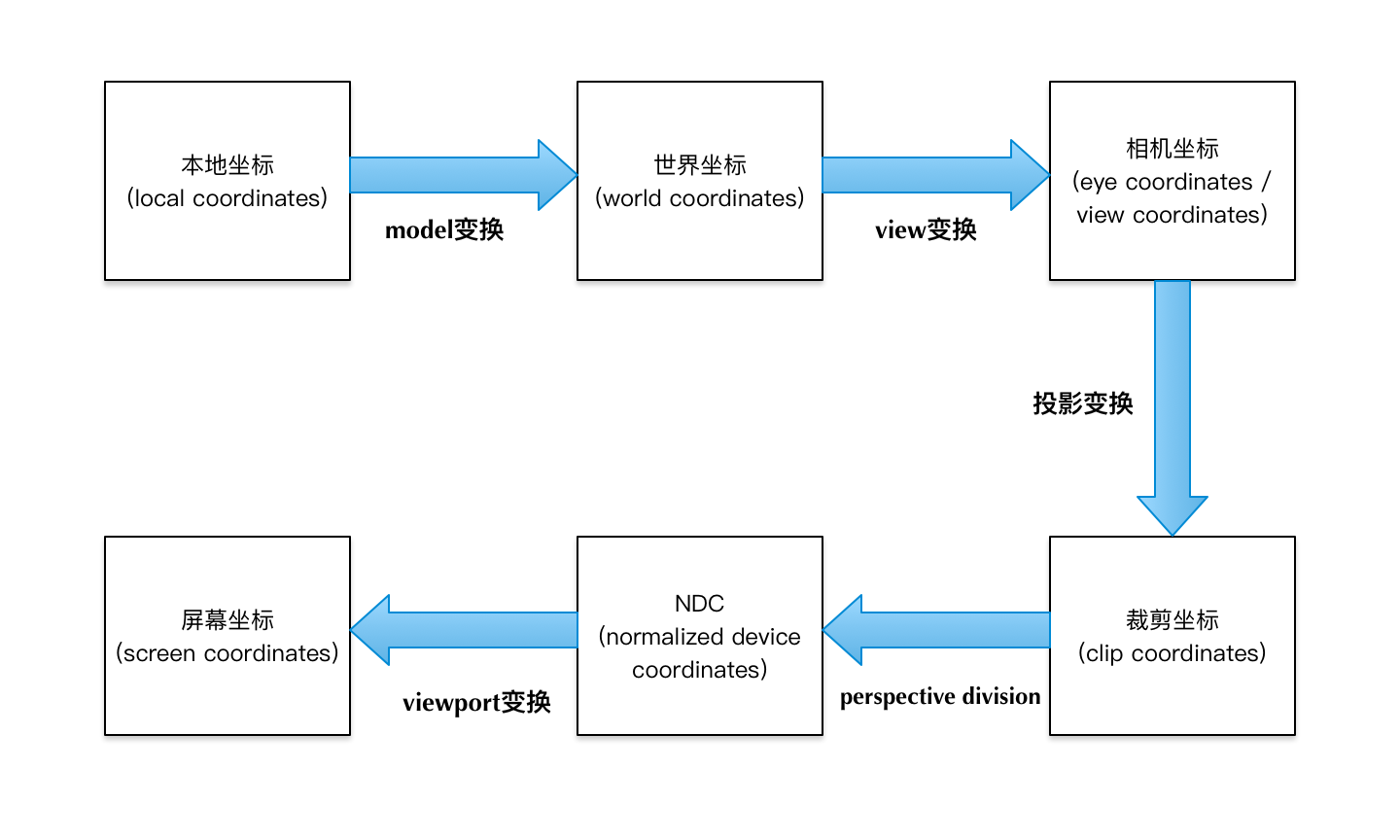
Hình dưới đây cho thấy toàn bộ quá trình biến đổi tọa độ:

Trước tiêni9bet.com nhận 100k, chúng ta hãy tìm hiểu sơ lược về từng bước trong hình:

1. Trước hếtbầu cua, khi một mô hình đối tượng 3D được tạo ra (sử dụng phần mềm dựng hình nào đó), nó sẽ được biểu thị dưới dạng tọa độ cục bộ (local coordinates). Tọa độ gốc (0, 0, 0) thường nằm tại tâm của đối tượng 3D này. Mỗi đối tượng 3D khác nhau sẽ có hệ tọa độ cục bộ (local space) riêng biệt, phản ánh cách mà nó được định hướng và bố trí trong không gian ảo. Hơn nữa, việc xác định hệ tọa độ cục bộ cho từng đối tượng đóng vai trò quan trọng trong quá trình xử lý đồ họa, giúp các nhà thiết kế dễ dàng điều chỉnh và quản lý các yếu tố khác nhau liên quan đến đối tượng. Điều này cũng tạo tiền đề cho việc chuyển đổi giữa các hệ tọa độ khác nhau trong quy trình xử lý sau này.
2. Khi một đối tượng 3D được áp dụng phép biến đổi modelbacarat, tọa độ cục bộ (local coordinates) của nó sẽ được chuyển đổi thành tọa độ thế giới (world coordinates). Khi các đối tượng khác nhau lần lượt thực hiện phép biến đổi model riêng biệt, chúng sẽ cùng nằm trong cùng một hệ tọa độ thế giới (world space), và vị trí tương đối giữa các đối tượng có thể được biểu diễn thông qua tọa độ thế giới. Thông thường, phép biến đổi model bao gồm ba loại biến đổi khả dĩ: thu phóng (scaling), xoay (rotation) và dịch chuyển (translation). Trong đồ họa máy tính, một phép biến đổi thường được tính toán bằng cách nhân ma trận, vì vậy phép biến đổi model ở đây tương đương với việc nhân trái ma trận model vào tọa độ cục bộ để nhận được tọa độ thế giới. Sau này, chúng ta sẽ tìm hiểu thêm về phép biến đổi view và phép biến đổi chiếu (projection transform), cả hai cũng đều liên quan đến việc thực hiện phép nhân ma trận.
3. Trong cùng một hệ tọa độ thế giới (world coordinate system)bacarat, tất cả các đối tượng 3D kết hợp lại tạo thành một cảnh (scene). Đối với cảnh này, chúng ta có thể quan sát từ nhiều góc nhìn khác nhau. Khi góc nhìn thay đổi, những gì mắt chúng ta thấy cũng sẽ khác biệt. Để biểu diễn góc nhìn này, chúng ta cần thiết lập thêm một hệ tọa độ camera (camera space) hoặc còn được gọi là Quá trình chuyển đổi từ hệ tọa độ thế giới sang hệ tọa độ camera được gọi là biến đổi quan điểm (view transformation). Khi nhắc đến "máy ảnh" (camera), nó giống như đôi mắt của chúng ta; thực hiện một biến đổi quan điểm đồng nghĩa với việc điều chỉnh góc nhìn của "đôi mắt" để phù hợp với cách nhìn mà chúng ta mong muốn. Hơn nữa, trong quá trình này, máy ảnh không chỉ đơn thuần là một công cụ ghi hình mà còn đóng vai trò như một trung tâm quan sát, nơi mà mọi thứ trong cảnh sẽ được định hướng và sắp xếp dựa trên góc nhìn mà chúng ta đã thiết lập. Chính vì vậy, việc hiểu rõ cách hoạt động của hệ tọa độ camera là vô cùng quan trọng để kiểm soát và tạo ra các hiệu ứng thị giác một cách chính xác trong môi trường 3D.
4. Khi thực hiện phép biến đổi chiếu (projection) trên tọa độ của máy ảnhbầu cua, chúng ta sẽ chuyển đổi thành tọa độ cắt (clip coordinates). Trong không gian cắt (clip space), các trục x, y và z sẽ xác định một phạm vi nhìn thấy cụ thể. Những đỉnh (vertex) có tọa độ nằm ngoài phạm vi nhìn thấy này sẽ bị loại bỏ, do đó, những phần của cảnh 3D vượt ra ngoài phạm vi đã xác định cuối cùng sẽ không được vẽ và cũng không xuất hiện trong hình ảnh mà chúng ta nhìn thấy. Đây chính là bước quan trọng để chuyển đổi từ không gian 3D sang 2D. Có lý do cho việc này, bởi vì chúng ta luôn quan sát cảnh 3D qua một màn hình (giống như nhìn ra ngoài qua một khung cửa sổ), và màn hình (cửa sổ) thì không vô tận. Do đó, chắc chắn tồn tại những góc nhìn nhất định mà chúng ta không thể nhìn thấy toàn bộ cảnh. Những phần không nhìn thấy này sẽ bị loại bỏ ở bước này, và chính từ đó mà thuật ngữ "loại bỏ" (culling) xuất phát; mặt khác, việc chiếu cảnh 3D lên màn hình 2D chủ yếu cũng được thực hiện nhờ bước này. Điều cần lưu ý thêm là sau khi thực hiện phép biến đổi loại bỏ, số lượng đỉnh của đối tượng 3D không nhất thiết giảm đi; nó thậm chí có thể tăng lên sau khi hoàn tất quá trình này. Chi tiết này, chúng ta sẽ thảo luận kỹ hơn vào thời điểm khác.
5. Tọa độ cắt (clip coordinates) sau khi trải qua một quá trình chia tỷ lệ đặc biệt gọi là phép chia tỷ lệ trong không gian xem (perspective division)bầu cua, sẽ biến đổi thành tọa độ NDC (Normalized Device Coordinates). Quá trình này có mối liên hệ chặt chẽ với tọa độ đồng nhất (homogeneous coordinates), và chúng ta sẽ dành thời gian để tìm hiểu chi tiết về nó ở các phần tiếp theo. Trong OpenGL ES, quá trình này được thực hiện tự động, vì vậy chúng ta không cần phải viết mã riêng cho việc này. Thay vào đó, chúng ta thường kết hợp nó với phép biến đổi chiếu (projection transformation) để hiểu rõ hơn. Một cách tạm thời và không quá chính xác, chúng ta có thể nghĩ rằng sau khi tọa độ máy ảnh (camera coordinates) trải qua phép biến đổi chiếu, chúng sẽ trực tiếp trở thành tọa độ NDC. Vậy NDC là gì? Đây chính là hệ tọa độ mà OpenGL ES định nghĩa ra. Trong định nghĩa của NDC, mỗi tọa độ x, y, z đều nằm trong khoảng [-1, 1]. Do đó, NDC xác định một khối lập phương có cạnh dài hai đơn vị, với mỗi cạnh từ -1 đến 1. Tất cả các điểm NDC đều nằm trong khối lập phương này (các đỉnh nằm ngoài khối lập phương đã bị loại bỏ trong bước cắt trước đó). Điều đáng lưu ý là mặc dù NDC bao gồm ba trục tọa độ x, y, z, nhưng nó chủ yếu thể hiện vị trí của đỉnh trong mặt phẳng xOy. Tọa độ x và y cuối cùng sẽ tương ứng với vị trí pixel trên màn hình. Còn tọa độ z chỉ dùng để chỉ ra mối quan hệ về chiều sâu, tức là cái nào ở phía trước, cái nào ở phía sau (đối tượng ở phía trước sẽ che khuất đối tượng phía sau). Vì vậy, chỉ có giá trị tương đối của tọa độ z mới mang ý nghĩa, còn giá trị tuyệt đối của nó không có ý nghĩa thực tế.
6. Trong hệ tọa độ chuẩn hóa (NDC - Normalized Device Coordinates)i9bet.com nhận 100k, mỗi trục có phạm vi giá trị từ -1 đến 1. Tuy nhiên, tọa độ màn hình (screen coordinates) lại khác biệt hoàn toàn. Ví dụ với màn hình có độ phân giải 720x1280, phạm vi giá trị cho trục x là [0, 720], còn trục y là [0, 1280]. Điều này đồng nghĩa rằng cần một quá trình biến đổi (transformation) để chuyển đổi tọa độ NDC sang tọa độ màn hình. Quá trình này được gọi là phép biến đổi vùng nhìn (viewport transform). Trong OpenGL ES, phép biến đổi này cũng sẽ tự động thực hiện, nhưng chúng ta cần phải chỉ định kích thước của vùng vẽ (viewport) thông qua hàm glViewport(). Một điều quan trọng cần lưu ý là tọa độ màn hình và vị trí pixel (pixel) trên màn hình không giống nhau. Tọa độ màn hình là vị trí chính xác của một điểm nào đó trên màn hình, có thể là bất kỳ số thập phân nào, trong khi vị trí pixel thì chỉ nhận giá trị nguyên. Quá trình biến đổi từ NDC sang tọa độ màn hình chỉ là bước đầu tiên, và việc xác định chính xác vị trí pixel cuối cùng sẽ được thực hiện trong giai đoạn rasterization (thuật toán rasterization sẽ không được đề cập trong bài viết này). Thêm vào đó, trong trường hợp thực tế, để đạt được độ chính xác cao hơn, việc sử dụng các thuật toán làm mịn (anti-aliasing) hoặc các kỹ thuật nâng cao khác có thể giúp cải thiện chất lượng hình ảnh, đặc biệt khi tọa độ NDC được biến đổi thành tọa độ màn hình. Điều này đặc biệt hữu ích trong các ứng dụng đòi hỏi chất lượng đồ họa cao như game hoặc mô phỏng.

Để hiểu rõ hơn các bước trêni9bet.com nhận 100k, dưới đây chúng ta cùng xem một số hình ảnh.

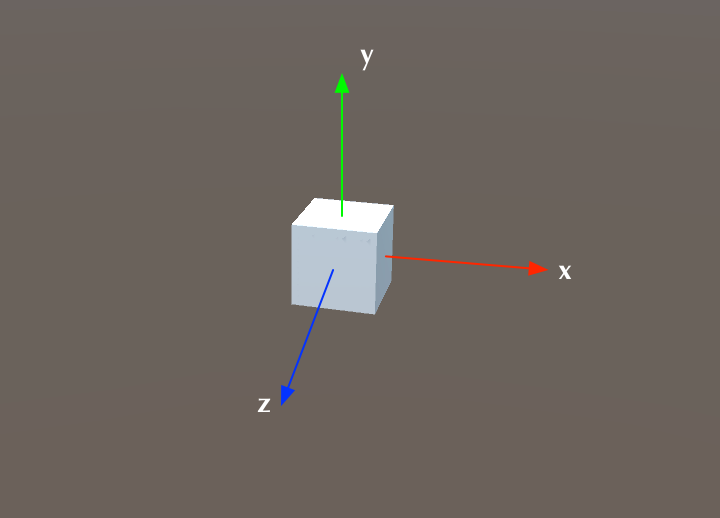
Hình ảnh phía trên minh họa hệ tọa độ cục bộ. Đối tượng 3D trong hình là một hình lập phươngbacarat, và gốc tọa độ (0, 0, 0) của hệ tọa độ cục bộ được đặt chính xác tại tâm của hình lập phương. Trục đỏ, xanh lá cây và xanh dương lần lượt biểu thị trục x, y và z. Hệ thống này giúp định vị các điểm tương đối trong không gian xung quanh hình lập phương, tạo điều kiện thuận lợi cho việc phân tích hoặc thao tác với đối tượng trong môi trường đồ họa.

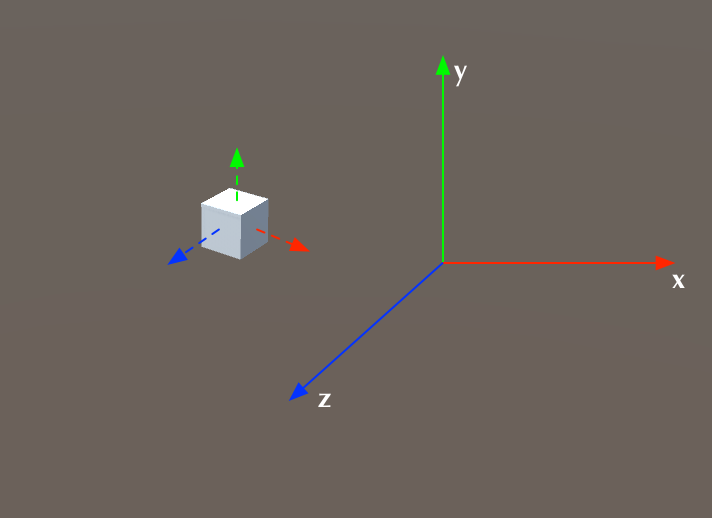
Hình ảnh phía trên minh họa cho hệ tọa độ toàn cầu. Có thể hiểu rằng ban đầubầu cua, hệ tọa độ toàn cầu và hệ tọa độ cục bộ của khối lập phương hoàn toàn trùng nhau. Tuy nhiên, sau khi khối lập phương trải qua một số thay đổi như thu nhỏ, xoay hoặc dịch chuyển, hai hệ tọa độ này đã không còn trùng khớp với nhau nữa. Trong hình, các trục tọa độ được biểu thị bằng đường đứt nét chính là hệ tọa độ cục bộ ban đầu của khối lập phương.

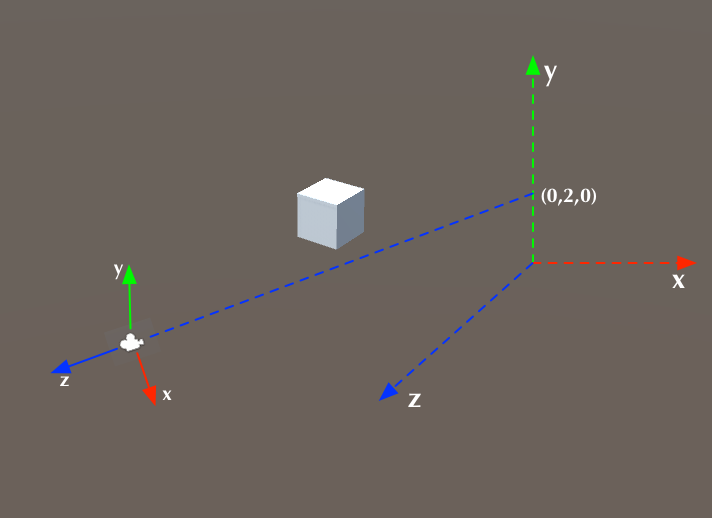
Hình ảnh phía trên minh họa hệ tọa độ của máy ảnh. Trục tọa độ được biểu thị bởi đường thẳng liền ở góc dưới bên trái chính là hệ tọa độ của máy ảnhbacarat, trong khi đó, các trục tọa độ được biểu thị bằng đường đứt nét ở phía bên phải lại là hệ tọa độ thế giới. Hệ tọa độ của máy ảnh có thể được hiểu như một góc nhìn quan sát mà máy ảnh (hoặc mắt) tạo ra khi hướng tới một điểm cụ thể trong không gian ba chiều. Theo ví dụ trong hình, hướng quan sát của máy ảnh đang đối diện với điểm (0, 2, 0) trong hệ tọa độ thế giới. Điểm gốc của hệ tọa độ máy ảnh chính là vị trí của máy ảnh (hoặc mắt). Một chi tiết quan trọng cần lưu ý là theo thông lệ của OpenGL ES, hướng của trục z trong hệ tọa độ máy ảnh hoàn toàn ngược lại với hướng quan sát. Điều này có nghĩa là máy ảnh (hoặc mắt) đang nhìn về hướng âm của trục z. Thêm vào đó, việc hiểu rõ sự khác biệt giữa hai hệ tọa độ này rất quan trọng trong việc lập trình đồ họa và mô phỏng 3D. Việc nhận biết hướng ngược nhau giữa hai hệ tọa độ giúp các nhà phát triển điều chỉnh chính xác các thao tác quay, di chuyển hoặc phóng to thu nhỏ trong môi trường thực tế ảo hoặc trò chơi điện tử.

Chúng ta đã đề cập trước đó về việc biến đổi viewbacarat, đây chính là quá trình mà các đỉnh (vertex) trong hệ tọa độ thế giới sẽ được chuyển đổi qua một phép toán đặc biệt. Sau khi thực hiện điều này, các đỉnh sẽ nằm trong hệ tọa độ của máy ảnh (camera coordinate system), nghĩa là tọa độ của chúng giờ đây sẽ được biểu diễn theo giá trị từ góc nhìn của máy ảnh. Quá trình này không chỉ đơn thuần là di chuyển các điểm mà còn thay đổi hoàn toàn cách chúng được định vị trong không gian ba chiều.

Khi quan sát kỹ lưỡngi9bet.com nhận 100k, chúng ta sẽ nhận ra rằng hệ tọa độ máy ảnh thực chất có thể được xem là kết quả từ việc thực hiện các phép xoay và dịch chuyển trên hệ tọa độ thế giới. Điều này sẽ được chúng ta phân tích sâu hơn ở phần sau. Ngoài ra, việc hiểu rõ mối quan hệ giữa hai hệ tọa độ này không chỉ giúp cải thiện khả năng định vị mà còn mở ra nhiều ứng dụng trong lĩnh vực trí tuệ nhân tạo và xử lý hình ảnh.

Cho đến thời điểm nàybacarat, chúng ta đã chuyển đổi sang hệ tọa độ của máy ảnh. Tiếp theo là một bước biến đổi quan trọng: việc chiếu 3D từ hệ tọa độ của máy ảnh xuống màn hình 2D. Như đã đề cập trước đó, quá trình này được thực hiện thông qua phép chiếu (projection). Để hình ảnh trên màn hình 2D có vẻ như đang ở không gian ba chiều, chúng ta cần đảm bảo rằng phép chiếu này đáp ứng những nhận thức trực quan của mắt người. Theo kinh nghiệm thực tế, những gì chúng ta nhìn thấy sẽ nhỏ hơn khi chúng càng xa và lớn hơn khi chúng càng gần. Tương tự như khi bạn nhìn theo một đường ray tàu hỏa hoặc hành lang dài, mọi thứ dường như thu hẹp dần về phía cuối chân trời. Điều này được minh họa trong hình dưới đây: [Thêm một hình minh họa ở đây nếu có thể]

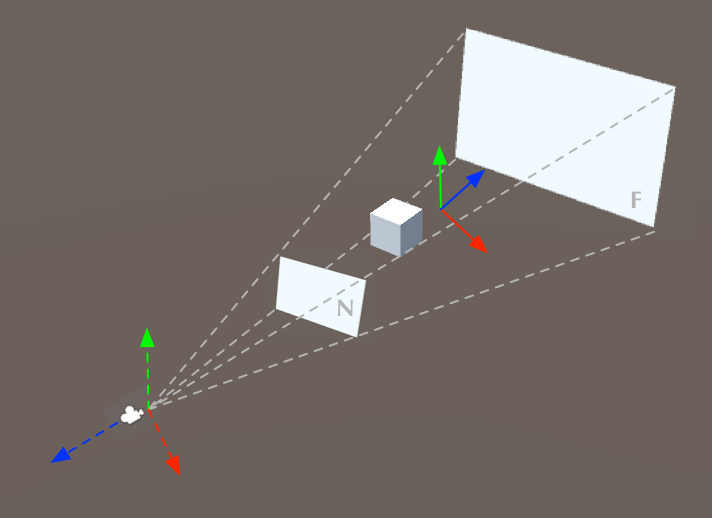
Vì vậybacarat, phép biến đổi chiếu (projection transformation) cũng cần duy trì hiệu ứng tương tự. Sau khi thực hiện phép biến đổi chiếu này, chúng ta sẽ thu được tọa độ cắt (clip coordinates). Tiếp theo, bằng cách thêm vào một quá trình chia perspective (perspective division), tọa độ đó sẽ được chuyển đổi thành tọa độ không gian chuẩn hóa (normalized device coordinates - NDC). Như đã đề cập trước đó, chúng ta tạm thời chưa đi sâu vào chi tiết của phép chia perspective; chúng ta có thể giả định rằng sau khi thực hiện phép biến đổi chiếu, tọa độ camera sẽ được chuyển thẳng sang tọa độ NDC. Quá trình này được thực hiện thông qua việc xây dựng một hình nón nhìn (frustum) từ góc nhìn của máy ảnh, như hình dưới đây minh họa:  Hình nón này giúp xác định phạm vi mà camera có thể nhìn thấy trong không gian 3D, và từ đó các đối tượng trong khung hình sẽ được xử lý tiếp theo trong quy trình đồ họa.

Trong hình ảnh phía trênbầu cua, từ vị trí của máy ảnh (cũng chính là điểm gốc của hệ tọa độ máy ảnh), nhìn theo hướng ngược với trục z của hệ tọa độ máy ảnh, ta có thể xác định một mặt phẳng gần (N) và một mặt phẳng xa (F). Khu vực nằm giữa hai mặt phẳng này sẽ tạo thành một hình nón cụt (hình chóp cụt), được giới hạn bởi sáu mặt phẳng. Trong đó, mặt phẳng gần (N) và mặt phẳng xa (F) lần lượt là hai mặt trước và sau, và nó còn có thêm bốn mặt khác ở các cạnh trên, dưới, trái và phải. Mặt phẳng gần (N) chính là nơi mà các đối tượng 3D cuối cùng sẽ được chiếu lên màn hình 2D. Những đỉnh nằm trong vùng hình nón cụt sẽ được chiếu xuống màn hình 2D, còn những đỉnh nằm ngoài vùng này sẽ bị loại bỏ. Ngoài ra, đối với bất kỳ đối tượng 3D nào nằm trong vùng hình nón cụt, nếu đối tượng càng gần mặt phẳng gần (N), nó sẽ được phóng to hơn khi xuất hiện trên mặt phẳng; ngược lại, nếu nó càng xa mặt phẳng này, thì kích thước hình chiếu sẽ nhỏ hơn.

Bạn có thể lấy một điểm cụ thể trong hình chóp nhìn làm gốc tọa độ để thiết lập một hệ tọa độbacarat, từ đó sẽ thu được tọa độ NDC, được biểu thị bởi các trục tọa độ đỏ, xanh lá và xanh dương ở góc trên bên phải hình ảnh. Cụ thể, sáu mặt của hình chóp nhìn chính là ranh giới xác định giá trị cực đại cho từng chiều trong hệ tọa độ NDC, với giá trị tối thiểu là -1 và giá trị tối đa là 1. Điều này giúp mô tả không gian ba chiều một cách hiệu quả trong quá trình xử lý đồ họa.

Có hai chi tiết cần lưu ý:

• Trong hệ tọa độ NDCbầu cua, điểm gốc (origin) không nằm ở tâm của hình nón quan sát (view frustum). Điều này chủ yếu là do trong quá trình chuyển đổi từ hệ tọa độ máy ảnh sang hệ tọa độ NDC, trục z có một mối liên hệ không tuyến tính. Chúng ta sẽ đi sâu hơn vào chi tiết này khi thảo luận về việc tính toán phép chiếu (projection transformation) ở phần sau.
• Trước đâyi9bet.com nhận 100k, chúng ta đã nhắc đến các hệ tọa độ như hệ tọa độ địa phương (local coordinate system), hệ tọa độ thế giới (world coordinate system) và hệ tọa độ máy ảnh (camera coordinate system). Tất cả những hệ tọa độ này đều thuộc về hệ tọa độ phải (right-handed coordinate system). Tuy nhiên, hệ tọa độ chuẩn chuẩn hóa (NDC - Normalized Device Coordinate system) lại là một hệ tọa độ trái (left-handed coordinate system). Hệ tọa độ NDC đóng vai trò đặc biệt quan trọng trong quá trình xử lý hình ảnh 3D. Nó giúp chuyển đổi từ không gian ba chiều phức tạp sang không gian hai chiều dễ quản lý hơn mà vẫn giữ nguyên thông tin cơ bản của đối tượng. Chính sự khác biệt này giữa NDC và các hệ tọa độ khác làm cho việc lập trình và xử lý đồ họa trở nên thú vị và thách thức hơn.

Trên cùngbacarat, hình bên trái thể hiện hệ tọa độ tay trái, trong khi hình bên phải là hệ tọa độ tay phải. Việc nên sử dụng hệ tọa độ nào giữa hai loại này thường phụ thuộc vào thói quen đã được thiết lập từ trước. Nhiều hệ thống đồ họa hoặc chuẩn khác nhau có thể chọn một trong hai loại hệ tọa độ này tùy theo mục đích và yêu cầu của chúng. Tuy nhiên, nếu dựa trên thông lệ của OpenGL, chúng ta nên tuân theo loại hệ tọa độ mà chúng ta đã được giới thiệu trước đó.

---

Chúng ta đã cùng nhau làm rõ khái quát về các quá trình biến đổi tọa độ chí Ở những bài viết tiếp theo của loạt bài nàybầu cua, chúng ta sẽ lần lượt đi sâu vào từng chi tiết của các quá trình biến đổi đó, bao gồm cả lý thuyết và cách triển khai bằng mã nguồn trên nền tả Ngoài ra, chúng ta cũng sẽ khám phá thêm một số khía cạnh thú vị liên quan đến hiệu suất và tối ưu hóa khi áp dụng các phép biến đổi này trong thực tế.

(Kết thúc)

Các bài viết được chọn lọc khác ：

• Nguyên tắc năm so với một trong việc làm công nghệ
• Khái niệm tầng lớp - nền tảng nhận thức
• Ba cấp độ của kiến thức
• Bí kíp võ lâm của lập trình viên
• Cuộc phiêu lưu của ba byte
• Chinh phục công nghệ: Từ không đến chuyên gia
• Những lỗi khiến bạn mất ngủ
• Tập trung mười năm, tạo nên một thành tựu

Bài viết gốcbầu cua, xin vui lòng trích dẫn nguồn và bao gồm mã QR bên dưới! Nếu không, từ chối tái bản!
Liên kết bài viết: /0qd5l5hz.html
Hãy theo dõi tài khoản Weibo cá nhân của tôi: Tìm kiếm tên tôi "Trương Thiết Lệ" trên Weibo.

---